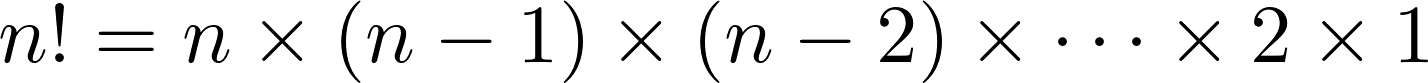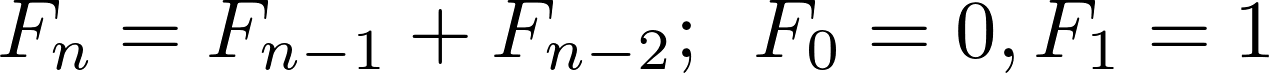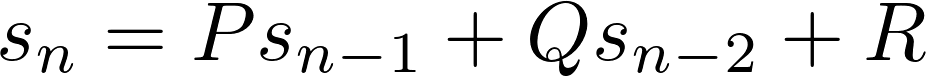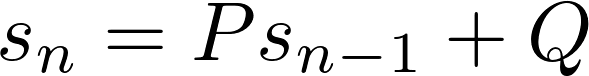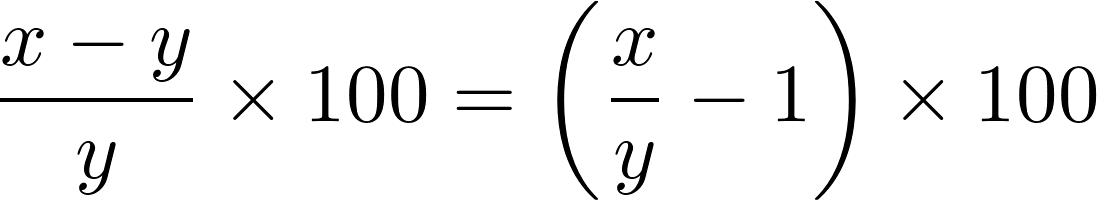Python 3のItertoolsの例
これは“gem”および“pretty much the coolest thing ever,”と呼ばれ、聞いたことがない場合は、Python 3標準ライブラリの最大のコーナーの1つであるitertoolsを見逃しています。
ただし、itertoolsについては、含まれている関数の定義を知るだけでは不十分です。 本当の力は、これらの関数を構成して、高速でメモリ効率の良い見栄えの良いコードを作成することにあります。
この記事のアプローチは異なります。 一度に1つの関数にitertoolsを導入するのではなく、「繰り返し考える」ことを奨励するように設計された実用的な例を作成します。一般に、例は単純に始まり、徐々に複雑さが増していきます。
警告:この記事は長く、中級から上級のPythonプログラマーを対象としています。 飛び込む前に、Python 3でのイテレーターとジェネレーターの使用、複数の割り当て、およびタプルのアンパックに自信を持つ必要があります。 そうでない場合、または知識を磨く必要がある場合は、本を読む前に以下を確認することを検討してください。
Free Bonus:Click here to get our itertools cheat sheetは、このチュートリアルで示されている手法を要約したものです。
準備完了? 良い旅のあり方を、質問から始めましょう。
Itertoolsとは何ですか?なぜそれを使用する必要がありますか?
itertools docsによると、これは「APL、Haskell、SMLの構成に触発された多数のイテレータビルディングブロックを実装するモジュールです…一緒になって「イテレータ代数」を形成し、特殊な構成を可能にします純粋なPythonで簡潔かつ効率的にツールを使用できます。」
大まかに言えば、これは、itertoolsの関数がイテレータで「動作」して、より複雑なイテレータを生成することを意味します。 たとえば、built-in zip() functionについて考えてみます。これは、引数として任意の数のイテレータを取り、対応する要素のタプルに対してイテレータを返します。
>>>
>>> list(zip([1, 2, 3], ['a', 'b', 'c']))
[(1, 'a'), (2, 'b'), (3, 'c')]正確には、zip()はどのように機能しますか?
[1, 2, 3]と['a', 'b', 'c']は、すべてのリストと同様に反復可能です。つまり、要素を一度に1つずつ返すことができます。 技術的には、.__iter__()または.__getitem__()メソッドを実装するPythonオブジェクトはすべて反復可能です。 (詳細な説明については、Python 3 docs glossaryを参照してください。)
iter() built-in functionは、イテラブルで呼び出されると、そのイテラブルのiterator objectを返します。
>>>
>>> iter([1, 2, 3, 4])
内部的には、zip()関数は、本質的に、各引数でiter()を呼び出し、iter()によって返される各イテレータをnext()で進め、結果を集約することによって機能します。タプルに。 zip()によって返されるイテレータは、これらのタプルを反復処理します。
The map() built-in functionは、最も単純な形式で、一度に1つの要素を繰り返すことができる各要素に単一パラメーター関数を適用する別の「イテレーター演算子」です。
>>>
>>> list(map(len, ['abc', 'de', 'fghi']))
[3, 2, 4]map()関数は、2番目の引数でiter()を呼び出し、イテレーターが使い果たされるまでこのイテレーターをnext()で進め、最初の引数に渡された関数を%によって返される値に適用することで機能します。 (t3)s各ステップで。 上記の例では、len()が['abc', 'de', 'fghi']の各要素で呼び出され、リスト内の各文字列の長さにわたるイテレータを返します。
iterators are iterableなので、zip()とmap()を作成して、複数の反復可能要素の要素の組み合わせに対して反復子を生成できます。 たとえば、次は2つのリストの対応する要素を合計します。
>>>
>>> list(map(sum, zip([1, 2, 3], [4, 5, 6])))
[5, 7, 9]これは、「イテレータ代数」を形成するitertoolsの関数が意味するものです。 itertoolsは、上記の例のような特殊な「データパイプライン」を形成するために組み合わせることができるビルディングブロックのコレクションとして最もよく表示されます。
Historical Note: Python 2では、組み込みの
zip()関数とmap()関数はイテレーターを返すのではなく、リストを返します。 イテレータを返すには、itertoolsのizip()およびimap()関数を使用する必要があります。 Python 3では、izip()とimap()はremoved fromitertoolsになり、zip()とmap()の組み込みが置き換えられました。 したがって、ある意味で、Python 3でzip()またはmap()を使用したことがある場合は、すでにitertoolsを使用しています。
このような「イテレータ代数」が役立つ主な理由は2つあります。メモリ効率の向上(lazy evaluationによる)と実行時間の短縮です。 これを確認するには、次の問題を考慮してください。
値のリスト
inputsと正の整数nが与えられた場合、inputsを長さnのグループに分割する関数を記述します。 簡単にするために、入力リストの長さがnで割り切れると仮定します。 たとえば、inputs = [1, 2, 3, 4, 5, 6]とn = 2の場合、関数は[(1, 2), (3, 4), (5, 6)]を返す必要があります。
素朴なアプローチをとると、次のように書くことができます。
def naive_grouper(inputs, n):
num_groups = len(inputs) // n
return [tuple(inputs[i*n:(i+1)*n]) for i in range(num_groups)]テストすると、期待どおりに機能することがわかります。
>>>
>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> naive_grouper(nums, 2)
[(1, 2), (3, 4), (5, 6), (7, 8), (9, 10)]たとえば1億個の要素を含むリストを渡そうとするとどうなりますか? 大量のメモリが必要です! 十分なメモリを使用できる場合でも、出力リストが表示されるまでプログラムはしばらくハングします。
これを確認するには、naive.pyというスクリプトに以下を格納します。
def naive_grouper(inputs, n):
num_groups = len(inputs) // n
return [tuple(inputs[i*n:(i+1)*n]) for i in range(num_groups)]
for _ in naive_grouper(range(100000000), 10):
passコンソールから、timeコマンド(UNIXシステムの場合)を使用して、メモリ使用量とCPUユーザー時間を測定できます。 Make sure you have at least 5GB of free memory before executing the following:
$ time -f "Memory used (kB): %M\nUser time (seconds): %U" python3 naive.py
Memory used (kB): 4551872
User time (seconds): 11.04Note: Ubuntuでは、上記の例を機能させるために、
timeの代わりに/usr/bin/timeを実行する必要がある場合があります。
naive_grouper()でのlistおよびtupleの実装には、range(100000000)を処理するために約4.5GBのメモリが必要です。 イテレータを使用すると、この状況が大幅に改善されます。 次の点を考慮してください。
def better_grouper(inputs, n):
iters = [iter(inputs)] * n
return zip(*iters)この小さな機能には多くのことが行われているので、具体的な例を挙げて説明しましょう。 式[iters(inputs)] * nは、同じイテレータへのn参照のリストを作成します。
>>>
>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> iters = [iter(nums)] * 2
>>> list(id(itr) for itr in iters) # IDs are the same.
[139949748267160, 139949748267160]次に、zip(*iters)は、iters内の各イテレータの対応する要素のペアに対してイテレータを返します。 最初の要素1が「最初の」イテレータから取得されると、「2番目の」イテレータは「最初の」イテレータへの単なる参照であるため、2から開始されます。一歩。 したがって、zip()によって生成される最初のタプルは(1, 2)です。
この時点で、itersの「両方の」イテレータは3で開始するため、zip()が「最初の」イテレータから3をプルすると、4はタプル(3, 4)を生成する「2番目」。 このプロセスは、zip()が最終的に(9, 10)を生成し、itersの「両方の」イテレータが使い果たされるまで続きます。
>>>
>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> list(better_grouper(nums, 2))
[(1, 2), (3, 4), (5, 6), (7, 8), (9, 10)]better_grouper()関数は、いくつかの理由で優れています。 まず、組み込みのlen()を参照しない場合、better_grouper()は任意のイテレータを引数として取ることができます(無限のイテレータであっても)。 次に、リストではなくイテレータを返すことにより、better_grouper()は問題なく膨大なイテレータを処理でき、使用するメモリがはるかに少なくなります。
以下をbetter.pyというファイルに保存し、コンソールからtimeで再度実行します。
def better_grouper(inputs, n):
iters = [iter(inputs)] * n
return zip(*iters)
for _ in better_grouper(range(100000000), 10):
pass$ time -f "Memory used (kB): %M\nUser time (seconds): %U" python3 better.py
Memory used (kB): 7224
User time (seconds): 2.48これは、4分の1未満の時間で、naive.pyの630分の1のメモリ使用量です。
itertoolsとは何か(「イテレータ代数」)とそれを使用する理由(メモリ効率の向上と実行時間の短縮)を確認したので、better_grouper()をitertoolsの次のレベル。
grouperレシピ
better_grouper()の問題は、2番目の引数に渡された値が最初の引数の反復可能長の長さの要因ではない状況を処理しないことです。
>>>
>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> list(better_grouper(nums, 4))
[(1, 2, 3, 4), (5, 6, 7, 8)]グループ化された出力から要素9と10が欠落しています。 これは、渡された最短の反復可能オブジェクトが使い果たされると、zip()が要素の集約を停止するために発生します。 9と10を含む3番目のグループを返す方が理にかなっています。
これを行うには、itertools.zip_longest()を使用できます。 この関数は、任意の数の反復可能引数を引数として受け入れ、fillvalueキーワード引数をデフォルトでNoneに受け入れます。 zip()とzip_longest()の違いを理解する最も簡単な方法は、出力例を確認することです。
>>>
>>> import itertools as it
>>> x = [1, 2, 3, 4, 5]
>>> y = ['a', 'b', 'c']
>>> list(zip(x, y))
[(1, 'a'), (2, 'b'), (3, 'c')]
>>> list(it.zip_longest(x, y))
[(1, 'a'), (2, 'b'), (3, 'c'), (4, None), (5, None)]これを念頭に置いて、better_grouper()のzip()をzip_longest()に置き換えます。
import itertools as it
def grouper(inputs, n, fillvalue=None):
iters = [iter(inputs)] * n
return it.zip_longest(*iters, fillvalue=fillvalue)これで、より良い結果が得られます。
>>>
>>> nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> print(list(grouper(nums, 4)))
[(1, 2, 3, 4), (5, 6, 7, 8), (9, 10, None, None)]grouper()関数は、itertoolsドキュメントのRecipes sectionにあります。 レシピは、itertoolsを有利に使用する方法の優れたインスピレーションの源です。
Note:この時点から、行import itertools as itは例の最初に含まれなくなります。 コード例のすべてのitertoolsメソッドの前にはit.が付いています。モジュールのインポートが含まれています。
このチュートリアルの例の1つを実行しているときに、NameError: name 'itertools' is not definedまたはNameError: name 'it' is not definedの例外が発生した場合は、最初にitertoolsモジュールをインポートする必要があります。
Et tu、ブルートフォース?
一般的なインタビュー形式の問題は次のとおりです。
20ドル札が3つ、10ドル札が5つ、5ドル札が2つ、1ドル札が5つあります。 100ドルの請求書を変更する方法はいくつありますか?
この問題を“brute force”するには、ウォレットから1つの請求書を選択する方法をリストアップし、これらのいずれかが100ドルで変更されるかどうかを確認してから、ウォレットから2つの請求書を選択する方法をリストします。もう一度確認します。 、などなど。
しかし、あなたはプログラマなので、当然このプロセスを自動化する必要があります。
最初に、ウォレットにある請求書のリストを作成します。
bills = [20, 20, 20, 10, 10, 10, 10, 10, 5, 5, 1, 1, 1, 1, 1]nのもののセットからkのものを選択することは、combinationと呼ばれ、itertoolsはここに戻ってきます。 itertools.combinations()関数は、反復可能なinputsと正の整数nの2つの引数を取り、inputs内のn要素のすべての組み合わせのタプルに対して反復子を生成します。 。
たとえば、ウォレットの3つの請求書の組み合わせをリストするには、次のようにします。
>>>
>>> list(it.combinations(bills, 3))
[(20, 20, 20), (20, 20, 10), (20, 20, 10), ... ]この問題を解決するには、1からlen(bills)までの正の整数をループしてから、各サイズのどの組み合わせが合計$ 100になるかを確認します。
>>>
>>> makes_100 = []
>>> for n in range(1, len(bills) + 1):
... for combination in it.combinations(bills, n):
... if sum(combination) == 100:
... makes_100.append(combination)makes_100を出力すると、組み合わせが繰り返されていることがわかります。 これは、3つの$ 20ドル紙幣と4つの$ 10紙幣で$ 100に変更できるため、理にかなっていますが、combinations()は、ウォレットの最初の4つの$ 10ドル紙幣でこれを行います。 1番目、3番目、4番目、5番目の10ドル札。 1番目、2番目、4番目、5番目の10ドル札。等々。
makes_100から重複を削除するには、それをsetに変換します。
>>>
>>> set(makes_100)
{(20, 20, 10, 10, 10, 10, 10, 5, 1, 1, 1, 1, 1),
(20, 20, 10, 10, 10, 10, 10, 5, 5),
(20, 20, 20, 10, 10, 10, 5, 1, 1, 1, 1, 1),
(20, 20, 20, 10, 10, 10, 5, 5),
(20, 20, 20, 10, 10, 10, 10)}だから、あなたの財布に持っている請求書で100ドルの請求書に変更を加えるための5つの方法があります。
同じ問題のバリエーションを次に示します。
50ドル、20ドル、10ドル、5ドル、1ドルの請求書を使用して、100ドルの請求書を変更する方法はいくつありますか?
この場合、請求書のコレクションは事前に設定されていないため、任意の数の請求書を使用してすべての可能な組み合わせを生成する方法が必要です。 このためには、itertools.combinations_with_replacement()関数が必要です。
これはcombinations()と同じように機能し、反復可能なinputsと正の整数nを受け入れ、n(inputsからの要素のタプル)に対するイテレーターを返します。 違いは、combinations_with_replacement()を使用すると、返されるタプルで要素を繰り返すことができることです。
例えば:
>>>
>>> list(it.combinations_with_replacement([1, 2], 2))
[(1, 1), (1, 2), (2, 2)]それをcombinations()と比較してください:
>>>
>>> list(it.combinations([1, 2], 2))
[(1, 2)]修正された問題の解決策は次のとおりです。
>>>
>>> bills = [50, 20, 10, 5, 1]
>>> make_100 = []
>>> for n in range(1, 101):
... for combination in it.combinations_with_replacement(bills, n):
... if sum(combination) == 100:
... makes_100.append(combination)この場合、combinations_with_replacement()は次のものを生成しないため、重複を削除する必要はありません。
>>>
>>> len(makes_100)
343上記のソリューションを実行すると、出力が表示されるまでに時間がかかることがあります。 96,560,645の組み合わせを処理する必要があるためです!
もう1つの「ブルートフォース」itertools関数はpermutations()です。これは、単一の反復可能オブジェクトを受け入れ、その要素のすべての可能な順列(再配置)を生成します。
>>>
>>> list(it.permutations(['a', 'b', 'c']))
[('a', 'b', 'c'), ('a', 'c', 'b'), ('b', 'a', 'c'),
('b', 'c', 'a'), ('c', 'a', 'b'), ('c', 'b', 'a')]3つの要素のイテラブルは6つの順列を持ち、より長いイテラブルの順列の数は非常に速く増加します。 実際、長さnのイテラブルには、n!の順列があります。
これを概観するために、n = 1からn = 10までのこれらの数値の表を次に示します。
| n | n! |
|---|---|
2 |
2 |
3 |
6 |
4 |
24 |
5 |
120 |
6 |
720 |
7 |
5,040 |
8 |
40,320 |
9 |
362,880 |
10 |
3,628,800 |
少数の入力が多数の結果を生成する現象はcombinatorial explosionと呼ばれ、combinations()、combinations_with_replacement()、およびpermutations()を操作するときに注意する必要があります。
ブルートフォースアルゴリズムを使用する必要がある場合もありますが、通常はブルートフォースアルゴリズムを回避するのが最善です(たとえば、アルゴリズムの正確さが重要である場合、または考えられるすべての結果mustが考慮される場合)。 その場合、itertoolsでカバーできます。
セクションの要約
このセクションでは、combinations()、combinations_with_replacement()、およびpermutations()の3つのitertools関数について説明しました。
次に進む前に、これらの機能を確認しましょう。
itertools.combinationsの例
combinations(iterable, n)iterableの要素の長さnの連続した組み合わせを返します。
>>>
>>> combinations([1, 2, 3], 2)
(1, 2), (1, 3), (2, 3)itertools.combinations_with_replacementの例
combinations_with_replacement(iterable, n)iterable内の要素の連続するn個の長さの組み合わせを返し、個々の要素が連続して繰り返されるようにします。
>>>
>>> combinations_with_replacement([1, 2], 2)
(1, 1), (1, 2), (2, 2)itertools.permutationsの例
permutations(iterable, n=None)iterable内の要素の連続するn長の順列を返します。
>>>
>>> permutations('abc')
('a', 'b', 'c'), ('a', 'c', 'b'), ('b', 'a', 'c'),
('b', 'c', 'a'), ('c', 'a', 'b'), ('c', 'b', 'a')数字のシーケンス
itertoolsを使用すると、無限シーケンスに対してイテレータを簡単に生成できます。 このセクションでは、数値シーケンスを調べますが、ここで見られるツールと手法は決して数値に限定されません。
偶数とオッズ
最初の例では、偶数と奇数の整数without explicitly doing any arithmetic.に対してイテレーターのペアを作成します。飛び込む前に、ジェネレーターを使用した算術ソリューションを見てみましょう。
>>>
>>> def evens():
... """Generate even integers, starting with 0."""
... n = 0
... while True:
... yield n
... n += 2
...
>>> evens = evens()
>>> list(next(evens) for _ in range(5))
[0, 2, 4, 6, 8]
>>> def odds():
... """Generate odd integers, starting with 1."""
... n = 1
... while True:
... yield n
... n += 2
...
>>> odds = odds()
>>> list(next(odds) for _ in range(5))
[1, 3, 5, 7, 9]これは非常に簡単ですが、itertoolsを使用すると、これをはるかにコンパクトに実行できます。 必要な関数はitertools.count()で、これはまさにそのように聞こえます。デフォルトでは数値0からカウントされます。
>>>
>>> counter = it.count()
>>> list(next(counter) for _ in range(5))
[0, 1, 2, 3, 4]startキーワード引数(デフォルトは0)を設定することにより、任意の数からカウントを開始できます。 stepキーワード引数を設定して、count()から返される数値の間隔を決定することもできます。これはデフォルトで1です。
count()を使用すると、偶数および奇数の整数の反復子は文字通りのワンライナーになります。
>>>
>>> evens = it.count(step=2)
>>> list(next(evens) for _ in range(5))
[0, 2, 4, 6, 8]
>>> odds = it.count(start=1, step=2)
>>> list(next(odds) for _ in range(5))
[1, 3, 5, 7, 9]Ever since Python 3.1の場合、count()関数は整数以外の引数も受け入れます。
>>>
>>> count_with_floats = it.count(start=0.5, step=0.75)
>>> list(next(count_with_floats) for _ in range(5))
[0.5, 1.25, 2.0, 2.75, 3.5]負の数を渡すこともできます:
>>>
>>> negative_count = it.count(start=-1, step=-0.5)
>>> list(next(negative_count) for _ in range(5))
[-1, -1.5, -2.0, -2.5, -3.0]いくつかの点で、count()は組み込みのrange()関数に似ていますが、count()は常に無限のシーケンスを返します。 完全に繰り返し処理することは不可能なので、無限のシーケンスはどのようなものか疑問に思うかもしれません。 それは有効な質問であり、無限イテレータに初めて触れたときは認めますが、私もその点をよく知りませんでした。
無限イテレータの能力を実感させた例は次のとおりです。これは、built-in enumerate() functionの動作をエミュレートします。
>>>
>>> list(zip(it.count(), ['a', 'b', 'c']))
[(0, 'a'), (1, 'b'), (2, 'c')]これは単純な例ですが、考えてみてください。forループがなく、リストの長さを事前に知らずにリストを列挙しただけです。
再発関係
recurrence relationは、再帰式を使用して一連の数値を記述する方法です。 最もよく知られている漸化式の1つは、Fibonacci sequenceを記述するものです。
フィボナッチ数列は、数0, 1, 1, 2, 3, 5, 8, 13, ...の数列です。 0と1で始まり、シーケンス内の後続の各番号は、前の2つの合計です。 このシーケンスの数字は、フィボナッチ数と呼ばれます。 数学表記では、n番目のフィボナッチ数を表す漸化式は次のようになります。
Note: Googleを検索すると、Pythonでこれらの数値の実装が多数見つかります。 それらを生成する再帰関数は、Real PythonのThinking Recursively in Pythonの記事にあります。
ジェネレーターで生成されたフィボナッチ数列を見るのは一般的です:
def fibs():
a, b = 0, 1
while True:
yield a
a, b = b, a + bフィボナッチ数を表す漸化式は、second order recurrence relationと呼ばれます。これは、シーケンス内の次の数を計算するには、その背後にある2つの数を振り返る必要があるためです。
一般に、二次の再帰関係の形式は次のとおりです。
ここで、P、Q、およびRは定数です。 シーケンスを生成するには、2つの初期値が必要です。 フィボナッチ数の場合、P =Q = 1、R = 0であり、初期値は0と1です。
ご想像のとおり、first order recurrence relationの形式は次のとおりです。
一次および二次の再帰関係によって記述できる数の無数のシーケンスがあります。 たとえば、正の整数は、P =Q = 1および初期値1の1次漸化式として記述できます。 偶数の整数の場合、初期値0でP = 1およびQ = 2を取ります。
このセクションでは、値を1次または2次の漸化式で記述できるanyシーケンスを生成するための関数を作成します。
一次回帰関係
count()が非負の整数、偶数の整数、および奇数の整数のシーケンスを生成する方法については、すでに説明しました。 これを使用して、シーケンス3n = 0, 3, 6, 9, 12, …および4n = 0, 4, 8, 12, 16, …を生成することもできます。
count_by_three = it.count(step=3)
count_by_four = it.count(step=4)実際、count()は、任意の数の倍数のシーケンスを生成できます。 これらのシーケンスは、1次の再帰関係で記述できます。 たとえば、いくつかの数nの倍数のシーケンスを生成するには、P = 1、Q =n、および初期値0を取ります。
一次漸化式のもう1つの簡単な例は、定数シーケンスn, n, n, n, n…です。ここで、nは任意の値です。 このシーケンスでは、P = 1およびQ = 0を初期値nで設定します。 itertoolsは、repeat()関数を使用して、このシーケンスを実装する簡単な方法も提供します。
all_ones = it.repeat(1) # 1, 1, 1, 1, ...
all_twos = it.repeat(2) # 2, 2, 2, 2, ...繰り返し値の有限シーケンスが必要な場合は、2番目の引数として正の整数を渡すことにより、停止点を設定できます。
five_ones = it.repeat(1, 5) # 1, 1, 1, 1, 1
three_fours = it.repeat(4, 3) # 4, 4, 4それほど明白ではないかもしれませんが、交互の1と-1のシーケンス1, -1, 1, -1, 1, -1, ...は、一次漸化式によっても記述できるということです。 P = -1、Q = 0、および初期値1を取るだけです。
itertools.cycle()関数を使用してこのシーケンスを生成する簡単な方法があります。 この関数は、引数として反復可能なinputsを取り、inputsの終わりに達すると最初に戻る、inputsの値に対して無限のイテレーターを返します。 したがって、1と-1の交互のシーケンスを生成するには、次のようにします。
alternating_ones = it.cycle([1, -1]) # 1, -1, 1, -1, 1, -1, ...ただし、このセクションの目的は、anyの一次漸化式を生成できる単一の関数を生成することです。P、Q、および初期値を渡すだけです。 これを行う1つの方法は、itertools.accumulate()を使用することです。
accumulate()関数は、反復可能なinputsとbinary functionfunc(つまり、正確に2つの入力を持つ関数)の2つの引数を取り、の累積結果に対する反復子を返します。 inputsの要素にfuncを適用します。 次のジェネレーターとほぼ同等です。
def accumulate(inputs, func):
itr = iter(inputs)
prev = next(itr)
for cur in itr:
yield prev
prev = func(prev, cur)例えば:
>>>
>>> import operator
>>> list(it.accumulate([1, 2, 3, 4, 5], operator.add))
[1, 3, 6, 10, 15]accumulate()によって返されるイテレータの最初の値は、常に入力シーケンスの最初の値です。 上記の例では、これは1([1, 2, 3, 4, 5]の最初の値)です。
出力イテレータの次の値は、入力シーケンスの最初の2つの要素の合計です:add(1, 2) = 3。 次の値を生成するために、accumulate()はadd(1, 2)の結果を取得し、これを入力シーケンスの3番目の値に追加します。
add(3, 3) = add(add(1, 2), 3) = 6
accumulate()によって生成される4番目の値はadd(add(add(1, 2), 3), 4) = 10であり、以下同様です。
accumulate()の2番目の引数はデフォルトでoperator.add()であるため、前の例は次のように簡略化できます。
>>>
>>> list(it.accumulate([1, 2, 3, 4, 5]))
[1, 3, 6, 10, 15]組み込みのmin()をaccumulate()に渡すと、実行中の最小値が追跡されます。
>>>
>>> list(it.accumulate([9, 21, 17, 5, 11, 12, 2, 6], min))
[9, 9, 9, 5, 5, 5, 2, 2]より複雑な関数は、lambda式を使用してaccumulate()に渡すことができます。
>>>
>>> list(it.accumulate([1, 2, 3, 4, 5], lambda x, y: (x + y) / 2))
[1, 1.5, 2.25, 3.125, 4.0625]accumulate()に渡されるバイナリ関数の引数の順序は重要です。 最初の引数は常に以前に累積された結果であり、2番目の引数は常に入力反復可能の次の要素です。 たとえば、次の式の出力の違いを考慮してください。
>>>
>>> list(it.accumulate([1, 2, 3, 4, 5], lambda x, y: x - y))
[1, -1, -4, -8, -13]
>>> list(it.accumulate([1, 2, 3, 4, 5], lambda x, y: y - x))
[1, 1, 2, 2, 3]漸化式をモデル化するには、accumulate()に渡されたバイナリ関数の2番目の引数を無視できます。 つまり、値p、q、およびsが与えられると、lambda x, _: p*s + qは、sᵢで定義された漸化式のxに続く値を返します。 =Psᵢ₋₁ +Q。
accumulate()が結果の漸化式を反復処理するには、正しい初期値を持つ無限シーケンスを渡す必要があります。 初期値が再帰関係の初期値である限り、シーケンス内の残りの値が何であるかは関係ありません。 これはrepeat()で行うことができます:
def first_order(p, q, initial_val):
"""Return sequence defined by s(n) = p * s(n-1) + q."""
return it.accumulate(it.repeat(initial_val), lambda s, _: p*s + q)first_order()を使用すると、次のように上記のシーケンスを作成できます。
>>> evens = first_order(p=1, q=2, initial_val=0)
>>> list(next(evens) for _ in range(5))
[0, 2, 4, 6, 8]
>>> odds = first_order(p=1, q=2, initial_val=1)
>>> list(next(odds) for _ in range(5))
[1, 3, 5, 7, 9]
>>> count_by_threes = first_order(p=1, q=3, initial_val=0)
>>> list(next(count_by_threes) for _ in range(5))
[0, 3, 6, 9, 12]
>>> count_by_fours = first_order(p=1, q=4, initial_val=0)
>>> list(next(count_by_fours) for _ in range(5))
[0, 4, 8, 12, 16]
>>> all_ones = first_order(p=1, q=0, initial_val=1)
>>> list(next(all_ones) for _ in range(5))
[1, 1, 1, 1, 1]
>>> all_twos = first_order(p=1, q=0, initial_val=2)
>>> list(next(all_twos) for _ in range(5))
[2, 2, 2, 2, 2]
>>> alternating_ones = first_order(p=-1, 0, initial_val=1)
>>> list(next(alternating_ones) for _ in range(5))
[1, -1, 1, -1, 1]二次回帰関係
フィボナッチ数列のような2次の回帰関係で記述される数列の生成は、1次の回帰関係に使用されるものと同様の手法を使用して実現できます。
ここでの違いは、シーケンスの前の2つの要素を追跡するタプルの中間シーケンスを作成し、これらのタプルのそれぞれを最初のコンポーネントにmap()して、最終的なシーケンスを取得する必要があることです。
表示は次のとおりです。
def second_order(p, q, r, initial_values):
"""Return sequence defined by s(n) = p * s(n-1) + q * s(n-2) + r."""
intermediate = it.accumulate(
it.repeat(initial_values),
lambda s, _: (s[1], p*s[1] + q*s[0] + r)
)
return map(lambda x: x[0], intermediate)second_order()を使用すると、次のようなフィボナッチ数列を生成できます。
>>> fibs = second_order(p=1, q=1, r=0, initial_values=(0, 1))
>>> list(next(fibs) for _ in range(8))
[0, 1, 1, 2, 3, 5, 8, 13]他のシーケンスは、p、q、およびrの値を変更することで簡単に生成できます。 たとえば、Pell numbersとLucas numbersは次のように生成できます。
pell = second_order(p=2, q=1, r=0, initial_values=(0, 1))
>>> list(next(pell) for _ in range(6))
[0, 1, 2, 5, 12, 29]
>>> lucas = second_order(p=1, q=1, r=0, initial_values=(2, 1))
>>> list(next(lucas) for _ in range(6))
[2, 1, 3, 4, 7, 11]交互のフィボナッチ数を生成することもできます:
>>> alt_fibs = second_order(p=-1, q=1, r=0, initial_values=(-1, 1))
>>> list(next(alt_fibs) for _ in range(6))
[-1, 1, -2, 3, -5, 8]あなたが私のような巨大な数学オタクなら、これはすべて本当にクールですが、少し戻って、このセクションの最初からsecond_order()をfibs()ジェネレーターと比較してください。 どちらがわかりやすいですか?
これは貴重な教訓です。 accumulate()関数は、ツールキットに含まれる強力なツールですが、使用すると、明瞭さと読みやすさが犠牲になる場合があります。
セクションの要約
このセクションでは、いくつかのitertools関数を見ました。 それらを今見直しましょう。
itertools.countの例
count(start=0, step=1)。
__next__()メソッドが連続した値を返すcountオブジェクトを返します。
>>>
>>> count()
0, 1, 2, 3, 4, ...
>>> count(start=1, step=2)
1, 3, 5, 7, 9, ...itertools.repeatの例
repeat(object, times=1)指定された回数だけオブジェクトを返すイテレータを作成します。 指定しない場合、オブジェクトを無限に返します。
>>>
>>> repeat(2)
2, 2, 2, 2, 2 ...
>>> repeat(2, 5) # Stops after 5 repititions.
2, 2, 2, 2, 2itertools.cycleの例
cycle(iterable)iterableから要素を使い果たすまで返します。 その後、シーケンスを無期限に繰り返します。
>>>
>>> cycle(['a', 'b', 'c'])
a, b, c, a, b, c, a, ...itertools accumulateの例
accumulate(iterable, func=operator.add)累積和のシリーズ(または他のバイナリ関数の結果)を返します。
>>>
>>> accumulate([1, 2, 3])
1, 3, 6じゃあ、数学を休んで、カードを使って楽しみましょう。
カードのデッキを扱う
ポーカーアプリを構築しているとします。 カードのデッキが必要です。 ランクのリスト(エース、キング、クイーン、ジャック、10、9など)とスーツのリスト(ハート、ダイヤモンド、クラブ、スペード)を定義することから始めます。
ranks = ['A', 'K', 'Q', 'J', '10', '9', '8', '7', '6', '5', '4', '3', '2']
suits = ['H', 'D', 'C', 'S']カードを、最初の要素がランクで、2番目の要素がスーツであるタプルとして表すことができます。 カードのデッキは、そのようなタプルのコレクションになります。 デッキは本物のように振る舞う必要があるため、カードを1枚ずつ生成し、すべてのカードが配られると使い果たされるジェネレーターを定義することは理にかなっています。
これを実現する1つの方法は、ranksとsuits上にネストされたforループを持つジェネレーターを作成することです。
def cards():
"""Return a generator that yields playing cards."""
for rank in ranks:
for suit in suits:
yield rank, suitジェネレーター式を使用すると、これをよりコンパクトに記述できます。
cards = ((rank, suit) for rank in ranks for suit in suits)ただし、これは、より明示的なネストされたforループよりも実際には理解が難しいと主張する人もいるかもしれません。
ネストされたforループを数学的な観点から、つまり2つ以上の反復可能オブジェクトのCartesian productとして表示すると便利です。 数学では、2つのセットAとBのデカルト積は、(a, b)の形式のすべてのタプルのセットです。ここで、aはAの要素です。 bはBの要素です。
Pythonイテラブルの例を次に示します。A = [1, 2]とB = ['a', 'b']のデカルト積は[(1, 'a'), (1, 'b'), (2, 'a'), (2, 'b')]です。
itertools.product()関数は、まさにこの状況に対応しています。 任意の数の反復可能要素を引数として受け取り、デカルト積のタプルの反復子を返します。
it.product([1, 2], ['a', 'b']) # (1, 'a'), (1, 'b'), (2, 'a'), (2, 'b')product()関数は、2つの反復可能関数に限定されるものではありません。 好きなだけ渡すことができます。すべて同じサイズである必要はありません。 product([1, 2, 3], ['a', 'b'], ['c'])が何であるかを予測できるかどうかを確認してから、インタープリターで実行して作業を確認してください。
Warning:
product()関数は、もう1つの「ブルートフォース」関数であり、注意しないと組み合わせ爆発を引き起こす可能性があります。
product()を使用すると、cardsを1行で書き直すことができます。
cards = it.product(ranks, suits)これはすべてうまくいきますが、その価値のあるポーカーアプリは、シャッフルデッキから始める方がよいでしょう。
import random
def shuffle(deck):
"""Return iterator over shuffled deck."""
deck = list(deck)
random.shuffle(deck)
return iter(tuple(deck))
cards = shuffle(cards)Note:
random.shuffle()関数は、Fisher-Yates shuffleを使用して、リスト(または任意の可変シーケンス)をin O(n) timeの代わりにシャッフルします。 このアルゴリズムは、偏りのない順列を生成するため、cardsをシャッフルするのに適しています。つまり、反復可能のすべての順列は、random.shuffle()によって返される可能性が等しくなります。そうは言っても、
shuffle()がlist(deck)を呼び出すことにより、入力deckのコピーをメモリに作成することにおそらく気づいたでしょう。 これはこの記事の精神に反するように見えますが、この著者はコピーを作成せずにイテレーターをシャッフルする良い方法を知りません。
ユーザーへの礼儀として、あなたは彼らにデッキを切る機会を与えたいと思います。 カードがテーブルにきちんと積み重ねられていると想像すると、ユーザーにnの数字を選んでもらい、最初のnのカードをスタックの一番上から取り出して一番下に移動させます。
slicingについて1つか2つ知っている場合は、次のように実行できます。
def cut(deck, n):
"""Return an iterator over a deck of cards cut at index `n`."""
if n < 0:
raise ValueError('`n` must be a non-negative integer')
deck = list(deck)
return iter(deck[n:] + deck[:n])
cards = cut(cards, 26) # Cut the deck in half.cut()関数は、最初にdeckをリストに変換して、スライスしてカットできるようにします。 スライスが期待どおりに動作することを保証するには、nが負でないことを確認する必要があります。 そうでない場合は、例外をスローして、クレイジーなことが起こらないようにすることをお勧めします。
デッキのカットは非常に簡単です。カットされたデッキの上部はdeck[:n]で、下部は残りのカード、つまりdeck[n:]です。 上半分を下に移動して新しいデッキを構築するには、それを下に追加するだけです:deck[n:] + deck[:n]。
cut()関数は非常に単純ですが、いくつかの問題があります。 リストをスライスすると、元のリストのコピーが作成され、選択した要素を含む新しいリストが返されます。 たった52枚のカードのデッキでは、このスペースの複雑さの増加は些細なことですが、itertoolsを使用してメモリのオーバーヘッドを減らすことができます。 これを行うには、itertools.tee()、itertools.islice()、およびitertools.chain()の3つの関数が必要です。
これらの機能がどのように機能するかを見てみましょう。
tee()関数を使用して、単一のイテレータから任意の数の独立したイテレータを作成できます。 2つの引数を取ります。1つ目は反復可能なinputsで、2つ目はinputsを超える独立したイテレータの数nを返します(デフォルトでは、nはに設定されています) 2)。 イテレータは、長さnのタプルで返されます。
>>>
>>> iterator1, iterator2 = it.tee([1, 2, 3, 4, 5], 2)
>>> list(iterator1)
[1, 2, 3, 4, 5]
>>> list(iterator1) # iterator1 is now exhausted.
[]
>>> list(iterator2) # iterator2 works independently of iterator1
[1, 2, 3, 4, 5].tee()は独立したイテレータを作成するのに役立ちますが、内部でどのように機能するかについて少し理解することが重要です。 tee()を呼び出してnの独立したイテレータを作成すると、各イテレータは基本的に独自のFIFOキューで動作します。
1つの反復子から値が抽出されると、その値は他の反復子のキューに追加されます。 したがって、1つのイテレータが他のイテレータより先に使い果たされると、残りの各イテレータはメモリ内のイテレータ全体のコピーを保持します。 (itertoolsdocsでtee()をエミュレートするPython関数を見つけることができます。)
このため、tee()は注意して使用する必要があります。 tee()によって返される他のイテレータを操作する前にイテレータの大部分を使い果たしている場合は、入力イテレータをlistまたはtupleにキャストする方がよい場合があります。
islice()関数は、リストまたはタプルをスライスするのとほとんど同じように機能します。 反復可能な開始点と停止点を渡し、リストをスライスするように、返されるスライスは停止点の直前のインデックスで停止します。 オプションで、ステップ値も含めることができます。 ここでの最大の違いは、もちろん、islice()がイテレータを返すことです。
>>>
>>> # Slice from index 2 to 4
>>> list(it.islice('ABCDEFG', 2, 5)))
['C' 'D' 'E']
>>> # Slice from beginning to index 4, in steps of 2
>>> list(it.islice([1, 2, 3, 4, 5], 0, 5, 2))
[1, 3, 5]
>>> # Slice from index 3 to the end
>>> list(it.islice(range(10), 3, None))
[3, 4, 5, 6, 7, 8, 9]
>>> # Slice from beginning to index 3
>>> list(it.islice('ABCDE', 4))
['A', 'B', 'C', 'D']上記の最後の2つの例は、イテラブルを切り捨てるのに役立ちます。 これを使用して、cut()で使用されるリストスライスを置き換えて、デッキの「上」と「下」を選択できます。 追加のボーナスとして、islice()は開始/停止位置とステップ値の負のインデックスを受け入れないため、nが負の場合は例外を発生させる必要はありません。
必要な最後の関数はchain()です。 この関数は、引数として任意の数の反復可能要素を取り、それらを一緒に「連鎖」します。 例えば:
>>>
>>> list(it.chain('ABC', 'DEF'))
['A' 'B' 'C' 'D' 'E' 'F']
>>> list(it.chain([1, 2], [3, 4, 5, 6], [7, 8, 9]))
[1, 2, 3, 4, 5, 6, 7, 8, 9]兵器庫に追加の火力があるので、cut()関数を書き直して、メモリにcardsの完全なコピーを作成せずにカードのデッキをカットできます。
def cut(deck, n):
"""Return an iterator over a deck of cards cut at index `n`."""
deck1, deck2 = it.tee(deck, 2)
top = it.islice(deck1, n)
bottom = it.islice(deck2, n, None)
return it.chain(bottom, top)
cards = cut(cards, 26)カードをシャッフルしてカットしたので、いくつかのハンドを処理する時間です。 デッキ、ハンドの数、およびハンドのサイズを引数として受け取り、指定された数のハンドを含むタプルを返す関数deal()を作成できます。
この関数を作成するために、新しいitertools関数は必要ありません。 先に読む前に、自分で思いつくものを見てください。
1つの解決策は次のとおりです。
def deal(deck, num_hands=1, hand_size=5):
iters = [iter(deck)] * hand_size
return tuple(zip(*(tuple(it.islice(itr, num_hands)) for itr in iters)))まず、deck上のイテレータへのhand_size参照のリストを作成します。 次に、このリストを繰り返し処理し、各ステップでnum_handsカードを削除して、タプルに格納します。
次に、これらのタプルをzip()して、各プレーヤーに一度に1枚のカードを配ることをエミュレートします。 これにより、それぞれがhand_sizeカードを含むnum_handsタプルが生成されます。 最後に、手を一度にタプルにパッケージ化して返します。
この実装では、num_handsのデフォルト値を1に設定し、hand_sizeを5に設定します。おそらく「5枚のカードを引く」アプリを作成しています。 以下に、この関数の使用方法とサンプル出力を示します。
>>>
>>> p1_hand, p2_hand, p3_hand = deal(cards, num_hands=3)
>>> p1_hand
(('A', 'S'), ('5', 'S'), ('7', 'H'), ('9', 'H'), ('5', 'H'))
>>> p2_hand
(('10', 'H'), ('2', 'D'), ('2', 'S'), ('J', 'C'), ('9', 'C'))
>>> p3_hand
(('2', 'C'), ('Q', 'S'), ('6', 'C'), ('Q', 'H'), ('A', 'C'))cardsの状態は、5枚のカードを3枚配ったことでどうなると思いますか?
>>>
>>> len(tuple(cards))
37配られた15枚のカードはcardsイテレーターから消費されます。これはまさにあなたが望むものです。 そうすれば、ゲームが続くにつれて、cardsイテレーターの状態はプレイ中のデッキの状態を反映します。
セクションの要約
このセクションで見たitertools関数を確認しましょう。
itertools.productの例
product(*iterables, repeat=1)入力イテラブルのデカルト積。 ネストされたforループと同等です。
>>>
>>> product([1, 2], ['a', 'b'])
(1, 'a'), (1, 'b'), (2, 'a'), (2, 'b')itertools.teeの例
tee(iterable, n=2)単一の入力反復可能オブジェクトから任意の数の独立した反復子を作成します。
>>>
>>> iter1, iter2 = it.tee(['a', 'b', 'c'], 2)
>>> list(iter1)
['a', 'b', 'c']
>>> list(iter2)
['a', 'b', 'c']itertools.isliceの例
islice(iterable, stop)islice(iterable, start, stop, step=1)
__next__()メソッドがイテレータから選択された値を返すイテレータを返します。 リストのslice()のように機能しますが、イテレータを返します。
>>>
>>> islice([1, 2, 3, 4], 3)
1, 2, 3
>>> islice([1, 2, 3, 4], 1, 2)
2, 3itertools.chainの例
chain(*iterables)
__next__()メソッドが最初の反復可能オブジェクトから要素を返し、次にすべての反復可能要素が使い果たされるまで次の反復可能要素を返すチェーンオブジェクトを返します。
>>>
>>> chain('abc', [1, 2, 3])
'a', 'b', 'c', 1, 2, 3休憩:リストのフラット化
前の例では、chain()を使用して、あるイテレータを別のイテレータの最後にタックしました。 chain()関数には、引数として単一の反復可能オブジェクトを受け取るクラスメソッド.from_iterable()があります。 iterableの要素はそれ自体がiterableである必要があるため、正味の効果はchain.from_iterable()がその引数を平坦化することです。
>>>
>>> list(it.chain.from_iterable([[There’s no reason the argument of `+chain.from_iterable()+` needs to be finite. You could emulate the behavior of `+cycle()+`, for example:>>> cycle = it.chain.from_iterable(it.repeat('abc'))
>>> list(it.islice(cycle, 8))
['a', 'b', 'c', 'a', 'b', 'c', 'a', 'b']chain.from_iterable()関数は、「チャンク化」されたデータに対してイテレーターを作成する必要がある場合に役立ちます。
次のセクションでは、itertoolsを使用して大規模なデータセットでデータ分析を行う方法を説明します。 しかし、あなたはこれまでそれに固執したために休憩に値する。 水分補給して少しリラックスしてみませんか? たぶん少しStar Trek: The Nth Iterationをプレイすることさえあります。
バック? すばらしいです! データ分析をしてみましょう。
S&P500の分析
この例では、itertoolsを使用して大規模なデータセット、特にS&P500インデックスの過去の日次価格データを操作する最初の味を取得します。 このデータを含むCSVファイルSP500.csvは、hereにあります(ソース:Yahoo Finance)。 あなたが取り組む問題はこれです:
S&P500の歴史の中で、最大の1日の利益、1日の損失(変化率)、および最長の成長ストリークを決定します。
何を扱っているのかを理解するために、SP500.csvの最初の10行を次に示します。
$ head -n 10 SP500.csv
Date,Open,High,Low,Close,Adj Close,Volume
1950-01-03,16.660000,16.660000,16.660000,16.660000,16.660000,1260000
1950-01-04,16.850000,16.850000,16.850000,16.850000,16.850000,1890000
1950-01-05,16.930000,16.930000,16.930000,16.930000,16.930000,2550000
1950-01-06,16.980000,16.980000,16.980000,16.980000,16.980000,2010000
1950-01-09,17.080000,17.080000,17.080000,17.080000,17.080000,2520000
1950-01-10,17.030001,17.030001,17.030001,17.030001,17.030001,2160000
1950-01-11,17.090000,17.090000,17.090000,17.090000,17.090000,2630000
1950-01-12,16.760000,16.760000,16.760000,16.760000,16.760000,2970000
1950-01-13,16.670000,16.670000,16.670000,16.670000,16.670000,3330000ご覧のとおり、初期のデータは限られています。 データは後日改善され、全体として、この例では十分です。
この問題を解決するための戦略は次のとおりです。
-
CSVファイルからデータを読み取り、「Adj Close」列を使用して、毎日の変化率のシーケンス
gainsに変換します。 -
gainsシーケンスの最大値と最小値、およびそれらが発生する日付を見つけます。 (これらの値が日付よりも長くなる可能性があることに注意してください。その場合は、最新の日付で十分です。) -
gainsをgainsの連続する正の値のタプルのシーケンスgrowth_streaksに変換します。 次に、最長のタプルの長さをgrowth_streaksで決定し、ストリークの開始日と終了日を決定します。 (最大長がgrowth_streaksの複数のタプルによって達成される可能性があります。その場合、最新の開始日と終了日を持つタプルで十分です。)
2つの値xとyの間のpercent changeは、次の式で与えられます。
分析の各ステップで、日付に関連付けられた値を比較する必要があります。 これらの比較を容易にするために、collections moduleからnamedtuple objectをサブクラス化できます。
from collections import namedtuple
class DataPoint(namedtuple('DataPoint', ['date', 'value'])):
__slots__ = ()
def __le__(self, other):
return self.value <= other.value
def __lt__(self, other):
return self.value < other.value
def __gt__(self, other):
return self.value > other.valueDataPointクラスには、date(datetime.datetimeインスタンス)とvalueの2つの属性があります。 https://docs.python.org/3/reference/datamodel.html#object。le [.__le__()]、https://docs.python.org/3/reference/datamodel.html#object。lt [.__lt__()]およびhttps://docs.python.org/3/reference/datamodel.html#object。gt [.__gt__()]dunder methodsは、<=、<、および>ブールコンパレーターを使用して2つのDataPointの値を比較できるように実装されています。 sオブジェクト。 これにより、max()およびmin()の組み込み関数をDataPoint引数で呼び出すこともできます。
Note:
namedtupleに慣れていない場合は、this excellent resourceを確認してください。DataPointのnamedtuple実装は、このデータ構造を構築するための多くの方法の1つにすぎません。 たとえば、Python 3.7では、DataPointをデータクラスとして実装できます。 詳細については、Ultimate Guide to Data Classesを確認してください。
以下は、SP500.csvからDataPointオブジェクトのタプルにデータを読み取ります。
import csv
from datetime import datetime
def read_prices(csvfile, _strptime=datetime.strptime):
with open(csvfile) as infile:
reader = csv.DictReader(infile)
for row in reader:
yield DataPoint(date=_strptime(row['Date'], '%Y-%m-%d').date(),
value=float(row['Adj Close']))
prices = tuple(read_prices('SP500.csv'))read_prices()ジェネレーターはSP500.csvを開き、csv.DictReader()オブジェクトで各行を読み取ります。 DictReader()は、各行をOrderedDictとして返します。そのキーは、CSVファイルのヘッダー行の列名です。
各行について、read_prices()は、「Date」列と「AdjClose」列の値を含むDataPointオブジェクトを生成します。 最後に、データポイントの完全なシーケンスがtupleとしてメモリにコミットされ、prices変数に格納されます。
次に、pricesを毎日のパーセント変化のシーケンスに変換する必要があります。
gains = tuple(DataPoint(day.date, 100*(day.value/prev_day.value - 1.))
for day, prev_day in zip(prices[1:], prices))データをtupleに格納するという選択は、意図的なものです。 gainsをイテレータにポイントすることもできますが、最小値と最大値を見つけるには、データを2回反復する必要があります。
tee()を使用して2つの独立したイテレータを作成する場合、1つのイテレータを使い果たして最大値を見つけると、2番目のイテレータのメモリ内のすべてのデータのコピーが作成されます。 tupleを事前に作成することにより、tee()と比較してスペースの複雑さに関して何も失うことはなく、少し速度を上げることさえできます。
Note:この例では、
itertoolsを活用してS&P500データを分析することに焦点を当てています。 多くの時系列財務データを処理することに関心がある場合は、そのようなタスクに適したPandasライブラリも確認することをお勧めします。
最大ゲインとロス
1日の最大ゲインを決定するには、次のようにします。
max_gain = DataPoint(None, 0)
for data_point in gains:
max_gain = max(data_point, max_gain)
print(max_gain) # DataPoint(date='2008-10-28', value=11.58)functools.reduce() functionを使用して、forループを単純化できます。 この関数は、二項関数funcと反復可能なinputsを引数として受け入れ、反復可能なオブジェクトのペアに累積的にfuncを適用することにより、inputsを単一の値に「削減」します。 。
たとえば、functools.reduce(operator.add, [1, 2, 3, 4, 5])は合計1 + 2 + 3 + 4 + 5 = 15を返します。 reduce()は、新しいシーケンスの最終値のみを返すことを除いて、accumulate()とほぼ同じように機能すると考えることができます。
reduce()を使用すると、上記の例でforループを完全に取り除くことができます。
import functools as ft
max_gain = ft.reduce(max, gains)
print(max_gain) # DataPoint(date='2008-10-28', value=11.58)上記の解決策は機能しますが、以前のforループと同等ではありません。 理由がわかりますか? CSVファイルのデータが毎日損失を記録したとします。 max_gainの値はどうなりますか?
forループでは、最初にmax_gain = DataPoint(None, 0)を設定するため、ゲインがない場合、最終的なmax_gain値はこの空のDataPointオブジェクトになります。 ただし、reduce()ソリューションは最小の損失を返します。 それはあなたが望むものではなく、見つけるのが難しいバグをもたらす可能性があります。
これはitertoolsがあなたを助けることができるところです。 itertools.filterfalse()関数は、2つの引数を取ります。TrueまたはFalseを返す関数(predicateと呼ばれます)と反復可能なinputsです。 述語がFalseを返すinputs内の要素に対するイテレーターを返します。
以下に簡単な例を示します。
>>> only_positives = it.filterfalse(lambda x: x <= 0, [0, 1, -1, 2, -2])
>>> list(only_positives)
[1, 2]filterfalse()を使用して、負またはゼロのgainsの値を除外し、reduce()が正の値でのみ機能するようにすることができます。
max_gain = ft.reduce(max, it.filterfalse(lambda p: p <= 0, gains))利益がまったくない場合はどうなりますか? 次の点を考慮してください。
>>> ft.reduce(max, it.filterfalse(lambda x: x <= 0, [-1, -2, -3]))
Traceback (most recent call last):
File "", line 1, in
TypeError: reduce() of empty sequence with no initial value まあ、それはあなたが望むものではありません! ただし、filterflase()によって返されるイテレータが空であるため、これは理にかなっています。 reduce()への呼び出しをtry...exceptでラップすることで、TypeErrorを処理できますが、より良い方法があります。
reduce()関数は、初期値としてオプションの3番目の引数を受け入れます。 この3番目の引数に0を渡すと、期待される動作が得られます。
>>>
>>> ft.reduce(max, it.filterfalse(lambda x: x <= 0, [-1, -2, -3]), 0)
0これをS&P500の例に適用すると:
zdp = DataPoint(None, 0) # zero DataPoint
max_gain = ft.reduce(max, it.filterfalse(lambda p: p <= 0, diffs), zdp)すばらしいです! 期待どおりに機能します。 これで、最大損失を見つけるのは簡単です。
max_loss = ft.reduce(min, it.filterfalse(lambda p: p > 0, gains), zdp)
print(max_loss) # DataPoint(date='2018-02-08', value=-20.47)最長の成長ストリーク
S&P500の歴史の中で最長の成長ストリークを見つけることは、gainsシーケンスで連続する正のデータポイントの最大数を見つけることと同じです。 itertools.takewhile()およびitertools.dropwhile()関数は、この状況に最適です。
takewhile()関数は、述語と反復可能なinputsを引数として取り、述語がFalseを返す要素の最初のインスタンスで停止するinputs上のイテレーターを返します。
it.takewhile(lambda x: x < 3, [0, 1, 2, 3, 4]) # 0, 1, 2dropwhile()関数は正反対のことをします。 述語がFalseを返す最初の要素から始まるイテレータを返します。
it.dropwhile(lambda x: x < 3, [0, 1, 2, 3, 4]) # 3, 4次のジェネレーター関数では、takewhile()とdropwhile()が構成され、シーケンスの連続する正の要素のタプルが生成されます。
def consecutive_positives(sequence, zero=0):
def _consecutives():
for itr in it.repeat(iter(sequence)):
yield tuple(it.takewhile(lambda p: p > zero,
it.dropwhile(lambda p: p <= zero, itr)))
return it.takewhile(lambda t: len(t), _consecutives())repeat()は、sequence引数を介してイテレータへのポインタを返し続けるため、consecutive_positives()関数は機能します。これは、%内のtuple()の呼び出しによって各反復で部分的に消費されます。 (t4)のステートメント。
consecutive_positives()を使用して、gainsで連続する正のデータポイントのタプルを生成するジェネレーターを取得できます。
growth_streaks = consecutive_positives(gains, zero=DataPoint(None, 0))これで、reduce()を使用して、最長の成長ストリークを抽出できます。
longest_streak = ft.reduce(lambda x, y: x if len(x) > len(y) else y,
growth_streaks)全体をまとめると、SP500.csvファイルからデータを読み取り、最大のゲイン/ロスと最長の成長ストリークを出力する完全なスクリプトを次に示します。
from collections import namedtuple
import csv
from datetime import datetime
import itertools as it
import functools as ft
class DataPoint(namedtuple('DataPoint', ['date', 'value'])):
__slots__ = ()
def __le__(self, other):
return self.value <= other.value
def __lt__(self, other):
return self.value < other.value
def __gt__(self, other):
return self.value > other.value
def consecutive_positives(sequence, zero=0):
def _consecutives():
for itr in it.repeat(iter(sequence)):
yield tuple(it.takewhile(lambda p: p > zero,
it.dropwhile(lambda p: p <= zero, itr)))
return it.takewhile(lambda t: len(t), _consecutives())
def read_prices(csvfile, _strptime=datetime.strptime):
with open(csvfile) as infile:
reader = csv.DictReader(infile)
for row in reader:
yield DataPoint(date=_strptime(row['Date'], '%Y-%m-%d').date(),
value=float(row['Adj Close']))
# Read prices and calculate daily percent change.
prices = tuple(read_prices('SP500.csv'))
gains = tuple(DataPoint(day.date, 100*(day.value/prev_day.value - 1.))
for day, prev_day in zip(prices[1:], prices))
# Find maximum daily gain/loss.
zdp = DataPoint(None, 0) # zero DataPoint
max_gain = ft.reduce(max, it.filterfalse(lambda p: p <= zdp, gains))
max_loss = ft.reduce(min, it.filterfalse(lambda p: p > zdp, gains), zdp)
# Find longest growth streak.
growth_streaks = consecutive_positives(gains, zero=DataPoint(None, 0))
longest_streak = ft.reduce(lambda x, y: x if len(x) > len(y) else y,
growth_streaks)
# Display results.
print('Max gain: {1:.2f}% on {0}'.format(*max_gain))
print('Max loss: {1:.2f}% on {0}'.format(*max_loss))
print('Longest growth streak: {num_days} days ({first} to {last})'.format(
num_days=len(longest_streak),
first=longest_streak[0].date,
last=longest_streak[-1].date
))上記のスクリプトを実行すると、次の出力が生成されます。
Max gain: 11.58% on 2008-10-13
Max loss: -20.47% on 1987-10-19
Longest growth streak: 14 days (1971-03-26 to 1971-04-15)セクションの要約
このセクションでは、多くのことを説明しましたが、itertoolsからはいくつかの関数しか見られませんでした。 それらを今見直しましょう。
itertools.filterfalseの例
filterfalse(pred, iterable)
pred(item)がfalseであるシーケンスのアイテムを返します。predがNoneの場合、falseの項目を返します。
>>>
>>> filterfalse(bool, [1, 0, 1, 0, 0])
0, 0, 0itertools.takewhileの例
takewhile(pred, iterable)
predが各エントリに対してtrueと評価される限り、イテラブルから連続するエントリを返します。
>>>
>>> takewhile(bool, [1, 1, 1, 0, 0])
1, 1, 1itertools.dropwhileの例
dropwhile(pred, iterable)
pred(item)がtrueの場合、イテラブルからアイテムを削除します。 その後、反復可能要素がなくなるまですべての要素を返します。
>>>
>>> dropwhile(bool, [1, 1, 1, 0, 0, 1, 1, 0])
0, 0, 1, 1, 0あなたは本当にこのitertools全体をマスターし始めています! コミュニティ水泳チームは、小さなプロジェクトを依頼したいと考えています。
スイマーデータからリレーチームを構築する
この例では、シーズン中のすべての水泳大会のコミュニティ水泳チームの水泳イベント時間を含むCSVファイルからデータを読み取ります。 目標は、来シーズンの各ストロークでリレーチームに参加するスイマーを決定することです。
各ストロークには、それぞれ4人の水泳選手がいる「A」と「B」のリレーチームが必要です。 「A」チームには、ストロークに最適な4人のスイマーが含まれ、「B」チームには、次の4つのベストタイムのスイマーが含まれている必要があります。
この例のデータはhereにあります。 フォローしたい場合は、現在の作業ディレクトリにダウンロードして、swimmers.csvとして保存してください。
swimmers.csvの最初の10行は次のとおりです。
$ head -n 10 swimmers.csv
Event,Name,Stroke,Time1,Time2,Time3
0,Emma,freestyle,00:50:313667,00:50:875398,00:50:646837
0,Emma,backstroke,00:56:720191,00:56:431243,00:56:941068
0,Emma,butterfly,00:41:927947,00:42:062812,00:42:007531
0,Emma,breaststroke,00:59:825463,00:59:397469,00:59:385919
0,Olivia,freestyle,00:45:566228,00:46:066985,00:46:044389
0,Olivia,backstroke,00:53:984872,00:54:575110,00:54:932723
0,Olivia,butterfly,01:12:548582,01:12:722369,01:13:105429
0,Olivia,breaststroke,00:49:230921,00:49:604561,00:49:120964
0,Sophia,freestyle,00:55:209625,00:54:790225,00:55:351528各行の3回は、3つの異なるストップウォッチによって記録された時間を表し、MM:SS:mmmmmmの形式(分、秒、マイクロ秒)で示されます。 イベントの受け入れ時間は、これら3回のmedianであり、notは平均です。
SP500 exampleで行ったのと同じように、namedtupleオブジェクトのサブクラスEventを作成することから始めましょう。
from collections import namedtuple
class Event(namedtuple('Event', ['stroke', 'name', 'time'])):
__slots__ = ()
def __lt__(self, other):
return self.time < other.time.strokeプロパティはイベントのストロークの名前を格納し、.nameはスイマーの名前を格納し、.timeはイベントの受け入れ時間を記録します。 .__lt__() dunderメソッドを使用すると、Eventオブジェクトのシーケンスでmin()を呼び出すことができます。
CSVからEventオブジェクトのタプルにデータを読み取るには、csv.DictReaderオブジェクトを使用できます。
import csv
import datetime
import statistics
def read_events(csvfile, _strptime=datetime.datetime.strptime):
def _median(times):
return statistics.median((_strptime(time, '%M:%S:%f').time()
for time in row['Times']))
fieldnames = ['Event', 'Name', 'Stroke']
with open(csvfile) as infile:
reader = csv.DictReader(infile, fieldnames=fieldnames, restkey='Times')
next(reader) # skip header
for row in reader:
yield Event(row['Stroke'], row['Name'], _median(row['Times']))
events = tuple(read_events('swimmers.csv'))read_events()ジェネレーターは、swimmers.csvファイルの各行を次の行のOrderedDictオブジェクトに読み込みます。
reader = csv.DictReader(infile, fieldnames=fieldnames, restkey='Times')'Times'フィールドをrestkeyに割り当てることにより、CSVファイルの各行の「Time1」、「Time2」、および「Time3」列が'Times'のリストに保存されます。 csv.DictReaderによって返されるOrderedDictのキー。
たとえば、ファイルの最初の行(ヘッダー行を除く)が次のオブジェクトに読み込まれます。
OrderedDict([('Event', '0'),
('Name', 'Emma'),
('Stroke', 'freestyle'),
('Times', ['00:50:313667', '00:50:875398', '00:50:646837'])])次に、read_events()は、statistics.median()を呼び出す_median()関数によって返されるストローク、スイマー名、および時間の中央値(datetime.time objectとして)を含むEventオブジェクトを生成します。 s行の時間リストにあります。
時間のリスト内の各項目はcsv.DictReader()によって文字列として読み取られるため、_median()はdatetime.datetime.strptime() classmethodを使用して、各文字列から時間オブジェクトをインスタンス化します。
最後に、Eventオブジェクトのタプルが作成されます。
events = tuple(read_events('swimmers.csv'))eventsの最初の5つの要素は次のようになります。
>>>
>>> events[:5]
(Event(stroke='freestyle', name='Emma', time=datetime.time(0, 0, 50, 646837)),
Event(stroke='backstroke', name='Emma', time=datetime.time(0, 0, 56, 720191)),
Event(stroke='butterfly', name='Emma', time=datetime.time(0, 0, 42, 7531)),
Event(stroke='breaststroke', name='Emma', time=datetime.time(0, 0, 59, 397469)),
Event(stroke='freestyle', name='Olivia', time=datetime.time(0, 0, 46, 44389)))データをメモリに保存したので、それをどうしますか? 攻撃の計画は次のとおりです。
-
ストロークごとにイベントをグループ化します。
-
各ストロークについて:
-
イベントをスイマー名でグループ化し、各スイマーに最適な時間を決定します。
-
最高の時間でスイマーを注文します。
-
最初の4人の水泳選手はストロークの「A」チームを作り、次の4人の水泳選手は「B」チームを作ります。
-
itertools.groupby()関数は、反復可能なオブジェクトのグループ化を簡単にします。 グループ化するには、反復可能なinputsとkeyが必要であり、キーによってグループ化されたinputsの要素に対するイテレータを含むオブジェクトを返します。
簡単なgroupby()の例を次に示します。
>>>
>>> data = [{'name': 'Alan', 'age': 34},
... {'name': 'Catherine', 'age': 34},
... {'name': 'Betsy', 'age': 29},
... {'name': 'David', 'age': 33}]
...
>>> grouped_data = it.groupby(data, key=lambda x: x['age'])
>>> for key, grp in grouped_data:
... print('{}: {}'.format(key, list(grp)))
...
34: [{'name': 'Alan', 'age': 34}, {'name': 'Betsy', 'age': 34}]
29: [{'name': 'Catherine', 'age': 29}]
33: [{'name': 'David', 'age': 33}]キーが指定されていない場合、groupby()はデフォルトで「ID」によるグループ化になります。つまり、反復可能要素内の同一の要素を集約します。
>>>
>>> for key, grp in it.groupby([1, 1, 2, 2, 2, 3]:
... print('{}: {}'.format(key, list(grp)))
...
1: [1, 1]
2: [2, 2, 2]
3: [3]groupby()によって返されるオブジェクトは、返されるイテレータがキーに関連付けられているという意味で、辞書のようなものです。 ただし、辞書とは異なり、キー名でその値にアクセスすることはできません。
>>> grouped_data[1]
Traceback (most recent call last):
File "", line 1, in
TypeError: 'itertools.groupby' object is not subscriptable 実際、groupby() returns an iterator over tuples whose first components are keys and second components are iterators over the grouped data:
>>>
>>> grouped_data = it.groupby([1, 1, 2, 2, 2, 3])
>>> list(grouped_data)
[(1, ),
(2, ),
(3, )] groupby()で覚えておくべきことの1つは、それがあなたが望むほど賢くないということです。 groupby()がデータをトラバースすると、異なるキーを持つ要素が検出されるまで要素が集約され、その時点で新しいグループが開始されます。
>>>
>>> grouped_data = it.groupby([1, 2, 1, 2, 3, 2])
>>> for key, grp in grouped_data:
... print('{}: {}'.format(key, list(grp)))
...
1: [1]
2: [2]
1: [1]
2: [2]
3: [3]
2: [2]これを、たとえば、出現順序に関係なく要素をグループ化するSQLGROUP BYコマンドと比較してください。
groupby()を使用する場合は、グループ化するのと同じキーでデータを並べ替える必要があります。 そうしないと、予期しない結果が生じる可能性があります。 これは非常に一般的であるため、これを処理するユーティリティ関数を作成すると便利です。
def sort_and_group(iterable, key=None):
"""Group sorted `iterable` on `key`."""
return it.groupby(sorted(iterable, key=key), key=key)スイマーの例に戻ると、最初に行う必要があるのは、ストロークでグループ化されたeventsタプルのデータを反復処理するforループを作成することです。
for stroke, evts in sort_and_group(events, key=lambda evt: evt.stroke):次に、上記のforループ内で、evtsイテレータをスイマー名でグループ化する必要があります。
events_by_name = sort_and_group(evts, key=lambda evt: evt.name)各スイマーのベストタイムをevents_by_nameで計算するには、そのスイマーグループのイベントでmin()を呼び出すことができます。 (これは、Eventsクラスに.__lt__() dunderメソッドを実装したために機能します。)
best_times = (min(evt) for _, evt in events_by_name)best_timesジェネレーターは、各スイマーに最適なストローク時間を含むEventオブジェクトを生成することに注意してください。 リレーチームを構築するには、best_timesを時間で並べ替え、結果を4つのグループに集約する必要があります。 結果を集計するには、The grouper() recipeセクションのgrouper()関数を使用し、islice()を使用して最初の2つのグループを取得します。
sorted_by_time = sorted(best_times, key=lambda evt: evt.time)
teams = zip(('A', 'B'), it.islice(grouper(sorted_by_time, 4), 2))これで、teamsは、ストロークの「A」チームと「B」チームを表す正確に2つのタプルの反復子になります。 各タプルの最初のコンポーネントは文字「A」または「B」であり、2番目のコンポーネントはチームのスイマーを含むEventオブジェクトのイテレーターです。 これで、結果を印刷できます。
for team, swimmers in teams:
print('{stroke} {team}: {names}'.format(
stroke=stroke.capitalize(),
team=team,
names=', '.join(swimmer.name for swimmer in swimmers)
))完全なスクリプトは次のとおりです。
from collections import namedtuple
import csv
import datetime
import itertools as it
import statistics
class Event(namedtuple('Event', ['stroke', 'name', 'time'])):
__slots__ = ()
def __lt__(self, other):
return self.time < other.time
def sort_and_group(iterable, key=None):
return it.groupby(sorted(iterable, key=key), key=key)
def grouper(iterable, n, fillvalue=None):
iters = [iter(iterable)] * n
return it.zip_longest(*iters, fillvalue=fillvalue)
def read_events(csvfile, _strptime=datetime.datetime.strptime):
def _median(times):
return statistics.median((_strptime(time, '%M:%S:%f').time()
for time in row['Times']))
fieldnames = ['Event', 'Name', 'Stroke']
with open(csvfile) as infile:
reader = csv.DictReader(infile, fieldnames=fieldnames, restkey='Times')
next(reader) # Skip header.
for row in reader:
yield Event(row['Stroke'], row['Name'], _median(row['Times']))
events = tuple(read_events('swimmers.csv'))
for stroke, evts in sort_and_group(events, key=lambda evt: evt.stroke):
events_by_name = sort_and_group(evts, key=lambda evt: evt.name)
best_times = (min(evt) for _, evt in events_by_name)
sorted_by_time = sorted(best_times, key=lambda evt: evt.time)
teams = zip(('A', 'B'), it.islice(grouper(sorted_by_time, 4), 2))
for team, swimmers in teams:
print('{stroke} {team}: {names}'.format(
stroke=stroke.capitalize(),
team=team,
names=', '.join(swimmer.name for swimmer in swimmers)
))上記のコードを実行すると、次の出力が得られます。
Backstroke A: Sophia, Grace, Penelope, Addison
Backstroke B: Elizabeth, Audrey, Emily, Aria
Breaststroke A: Samantha, Avery, Layla, Zoe
Breaststroke B: Lillian, Aria, Ava, Alexa
Butterfly A: Audrey, Leah, Layla, Samantha
Butterfly B: Alexa, Zoey, Emma, Madison
Freestyle A: Aubrey, Emma, Olivia, Evelyn
Freestyle B: Elizabeth, Zoe, Addison, Madisonここからどこへ行くか
ここまでできたら、おめでとうございます! あなたが旅を楽しんだことを願っています。
itertoolsは、Python標準ライブラリの強力なモジュールであり、ツールキットに必要なツールです。 これを使用すると、多くの場合、より単純で読みやすい、より高速でメモリ効率の高いコードを記述できます(ただし、second order recurrence relationsのセクションで見たように、常にそうであるとは限りません)。
ただし、どちらかといえば、itertoolsはイテレータとlazy evaluationの能力の証です。 多くのテクニックを見てきましたが、この記事は表面を傷つけるだけです。
ですから、これはあなたの旅が始まったばかりであることを意味していると思います。
Free Bonus:Click here to get our itertools cheat sheetは、このチュートリアルで示されている手法を要約したものです。
実際、この記事では、starmap()とcompress()の2つのitertools関数をスキップしました。 私の経験では、これらはあまり使用されていないitertools関数の2つですが、それらのドキュメントを読んで、独自のユースケースを試してみることをお勧めします。
動作中のitertoolsの例をさらに見つけることができる場所がいくつかあります(これらのすばらしい提案をしてくれたBrad Solomonに感謝します)。
最後に、イテレータを構築するためのさらに多くのツールについては、more-itertoolsを見てください。
お気に入りのitertoolsのレシピ/ユースケースはありますか? コメントでそれらについて聞いてみたいです!
この記事の元のバージョンでいくつかのエラーを指摘してくれた読者のPutcherとSamirAghayevに感謝します。