Pythonヒストグラムプロット：NumPy、Matplotlib、Pandas＆Seaborn

>>> # Need not be sorted, necessarily
>>> a = (0, 1, 1, 1, 2, 3, 7, 7, 23)

>>> def count_elements(seq) -> dict:
...     """Tally elements from `seq`."""
...     hist = {}
...     for i in seq:
...         hist[i] = hist.get(i, 0) + 1
...     return hist

>>> counted = count_elements(a)
>>> counted
{0: 1, 1: 3, 2: 1, 3: 1, 7: 2, 23: 1}

>>> from collections import Counter

>>> recounted = Counter(a)
>>> recounted
Counter({0: 1, 1: 3, 3: 1, 2: 1, 7: 2, 23: 1})

>>> recounted.items() == counted.items()
True

def ascii_histogram(seq) -> None:
    """A horizontal frequency-table/histogram plot."""
    counted = count_elements(seq)
    for k in sorted(counted):
        print('{0:5d} {1}'.format(k, '+' * counted[k]))

>>> # No NumPy ... yet
>>> import random
>>> random.seed(1)

>>> vals = [1, 3, 4, 6, 8, 9, 10]
>>> # Each number in `vals` will occur between 5 and 15 times.
>>> freq = (random.randint(5, 15) for _ in vals)

>>> data = []
>>> for f, v in zip(freq, vals):
...     data.extend([v] * f)

>>> ascii_histogram(data)
    1 +++++++
    3 ++++++++++++++
    4 ++++++
    6 +++++++++
    8 ++++++
    9 ++++++++++++
   10 ++++++++++++

>>> import numpy as np
>>> # `numpy.random` uses its own PRNG.
>>> np.random.seed(444)
>>> np.set_printoptions(precision=3)

>>> d = np.random.laplace(loc=15, scale=3, size=500)
>>> d[:5]
array([18.406, 18.087, 16.004, 16.221,  7.358])

>>> hist, bin_edges = np.histogram(d)

>>> hist
array([ 1,  0,  3,  4,  4, 10, 13,  9,  2,  4])

>>> bin_edges
array([ 3.217,  5.199,  7.181,  9.163, 11.145, 13.127, 15.109, 17.091,
       19.073, 21.055, 23.037])

>>> hist.size, bin_edges.size
(10, 11)

>>> # The leftmost and rightmost bin edges
>>> first_edge, last_edge = a.min(), a.max()

>>> n_equal_bins = 10  # NumPy's default
>>> bin_edges = np.linspace(start=first_edge, stop=last_edge,
...                         num=n_equal_bins + 1, endpoint=True)
...
>>> bin_edges
array([ 0. ,  2.3,  4.6,  6.9,  9.2, 11.5, 13.8, 16.1, 18.4, 20.7, 23. ])

>>> bcounts = np.bincount(a)
>>> hist, _ = np.histogram(a, range=(0, a.max()), bins=a.max() + 1)

>>> np.array_equal(hist, bcounts)
True

>>> # Reproducing `collections.Counter`
>>> dict(zip(np.unique(a), bcounts[bcounts.nonzero()]))
{0: 1, 1: 3, 2: 1, 3: 1, 7: 2, 23: 1}

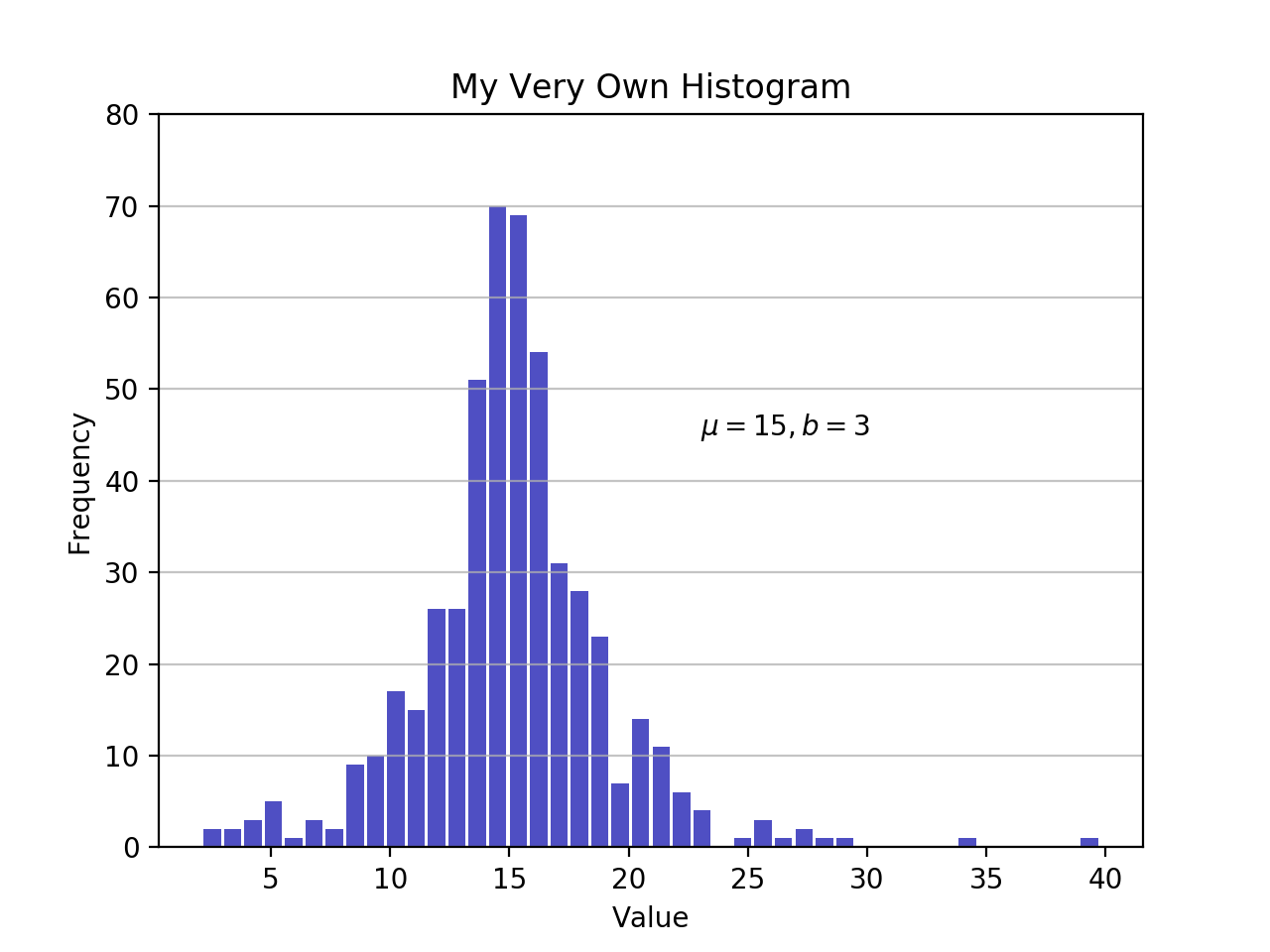
import matplotlib.pyplot as plt

# An "interface" to matplotlib.axes.Axes.hist() method
n, bins, patches = plt.hist(x=d, bins='auto', color='#0504aa',
                            alpha=0.7, rwidth=0.85)
plt.grid(axis='y', alpha=0.75)
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.title('My Very Own Histogram')
plt.text(23, 45, r'$\mu=15, b=3$')
maxfreq = n.max()
# Set a clean upper y-axis limit.
plt.ylim(ymax=np.ceil(maxfreq / 10) * 10 if maxfreq % 10 else maxfreq + 10)

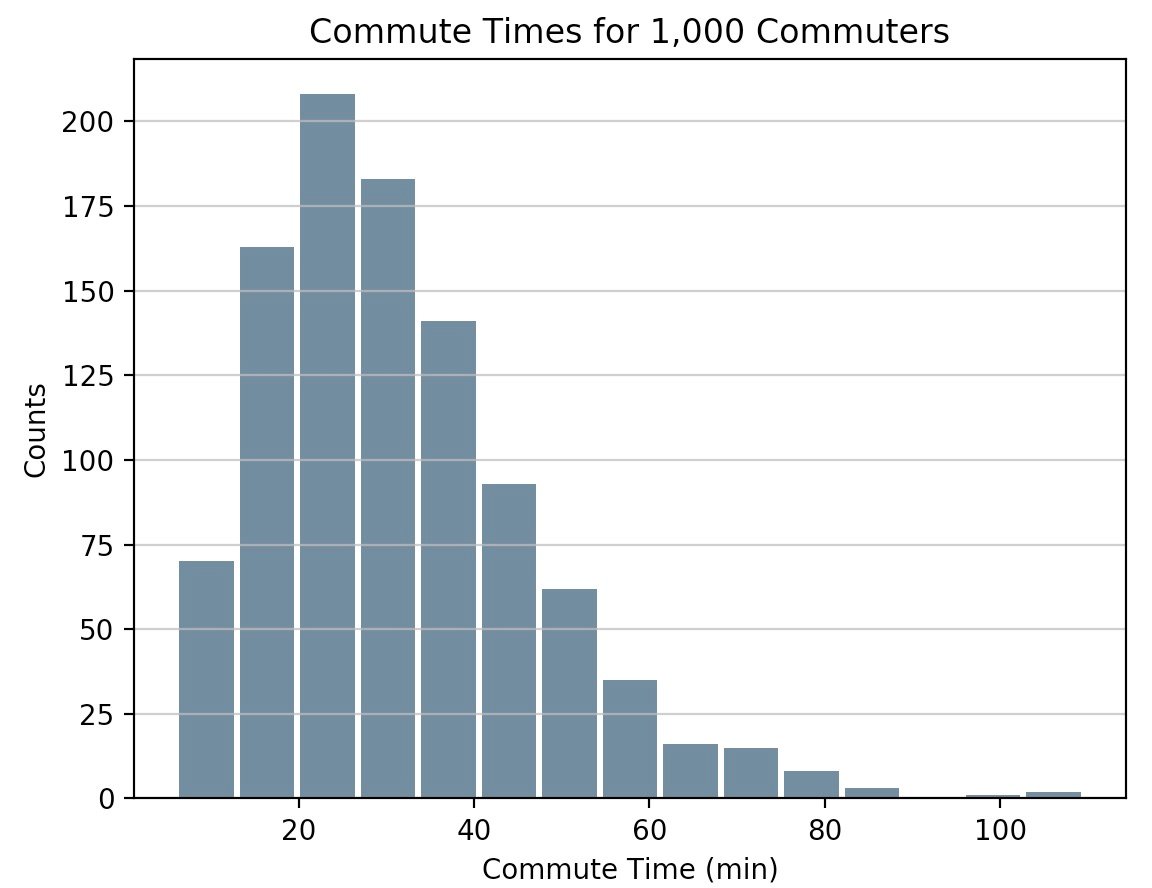
import pandas as pd

# Generate data on commute times.
size, scale = 1000, 10
commutes = pd.Series(np.random.gamma(scale, size=size) ** 1.5)

commutes.plot.hist(grid=True, bins=20, rwidth=0.9,
                   color='#607c8e')
plt.title('Commute Times for 1,000 Commuters')
plt.xlabel('Counts')
plt.ylabel('Commute Time')
plt.grid(axis='y', alpha=0.75)

>>> # Sample from two different normal distributions
>>> means = 10, 20
>>> stdevs = 4, 2
>>> dist = pd.DataFrame(
...     np.random.normal(loc=means, scale=stdevs, size=(1000, 2)),
...     columns=['a', 'b'])
>>> dist.agg(['min', 'max', 'mean', 'std']).round(decimals=2)
          a      b
min   -1.57  12.46
max   25.32  26.44
mean  10.12  19.94
std    3.94   1.94

fig, ax = plt.subplots()
dist.plot.kde(ax=ax, legend=False, title='Histogram: A vs. B')
dist.plot.hist(density=True, ax=ax)
ax.set_ylabel('Probability')
ax.grid(axis='y')
ax.set_facecolor('#d8dcd6')

from scipy import stats

# An object representing the "frozen" analytical distribution
# Defaults to the standard normal distribution, N~(0, 1)
dist = stats.norm()

# Draw random samples from the population you built above.
# This is just a sample, so the mean and std. deviation should
# be close to (1, 0).
samp = dist.rvs(size=1000)

# `ppf()`: percent point function (inverse of cdf — percentiles).
x = np.linspace(start=stats.norm.ppf(0.01),
                stop=stats.norm.ppf(0.99), num=250)
gkde = stats.gaussian_kde(dataset=samp)

# `gkde.evaluate()` estimates the PDF itself.
fig, ax = plt.subplots()
ax.plot(x, dist.pdf(x), linestyle='solid', c='red', lw=3,
        alpha=0.8, label='Analytical (True) PDF')
ax.plot(x, gkde.evaluate(x), linestyle='dashed', c='black', lw=2,
        label='PDF Estimated via KDE')
ax.legend(loc='best', frameon=False)
ax.set_title('Analytical vs. Estimated PDF')
ax.set_ylabel('Probability')
ax.text(-2., 0.35, r'$f(x) = \frac{\exp(-x^2/2)}{\sqrt{2*\pi}}$',
        fontsize=12)

import seaborn as sns

sns.set_style('darkgrid')
sns.distplot(d)

sns.distplot(d, fit=stats.laplace, kde=False)

>>> import pandas as pd

>>> data = np.random.choice(np.arange(10), size=10000,
...                         p=np.linspace(1, 11, 10) / 60)
>>> s = pd.Series(data)

>>> s.value_counts()
9    1831
8    1624
7    1423
6    1323
5    1089
4     888
3     770
2     535
1     347
0     170
dtype: int64

>>> s.value_counts(normalize=True).head()
9    0.1831
8    0.1624
7    0.1423
6    0.1323
5    0.1089
dtype: float64

>>> ages = pd.Series(
...     [1, 1, 3, 5, 8, 10, 12, 15, 18, 18, 19, 20, 25, 30, 40, 51, 52])
>>> bins = (0, 10, 13, 18, 21, np.inf)  # The edges
>>> labels = ('child', 'preteen', 'teen', 'military_age', 'adult')
>>> groups = pd.cut(ages, bins=bins, labels=labels)

>>> groups.value_counts()
child           6
adult           5
teen            3
military_age    2
preteen         1
dtype: int64

>>> pd.concat((ages, groups), axis=1).rename(columns={0: 'age', 1: 'group'})
    age         group
0     1         child
1     1         child
2     3         child
3     5         child
4     8         child
5    10         child
6    12       preteen
7    15          teen
8    18          teen
9    18          teen
10   19  military_age
11   20  military_age
12   25         adult
13   30         adult
14   40         adult
15   51         adult
16   52         adult