前書き
時系列は、将来の価値を予測する機会を提供します。 以前の値に基づいて、時系列を使用して、経済学、天気、およびキャパシティプランニングの傾向を予測できます。 時系列データの特定のプロパティは、通常、特殊な統計的手法が必要であることを意味します。
このチュートリアルでは、時系列の信頼できる予測を作成することを目指します。 自己相関、定常性、季節性の概念を紹介して議論することから始め、ARIMAとして知られる時系列予測に最も一般的に使用される方法の1つを適用します。
時系列の将来のポイントをモデル化および予測するためにPythonで使用できるメソッドの1つは、Seasonal AutoRegressive Integrated Moving Averages with eXogenous regressorsを表すSARIMAXとして知られています。 ここでは、主にARIMAコンポーネントに注目します。これは、時系列データを近似して、時系列の将来のポイントをよりよく理解および予測するために使用されます。
前提条件
このガイドでは、ローカルデスクトップまたはリモートサーバーで時系列分析を行う方法について説明します。 大規模なデータセットの操作はメモリを大量に消費する可能性があるため、いずれの場合も、このガイドの計算の一部を実行するには、コンピューターに少なくとも2GB of memoryが必要です。
このチュートリアルを最大限に活用するには、時系列と統計に関するある程度の知識が役立ちます。
このチュートリアルでは、Jupyter Notebookを使用してデータを操作します。 まだお持ちでない場合は、tutorial to install and set up Jupyter Notebook for Python 3に従ってください。
[[step-1 -—- installing-packages]] ==ステップ1—パッケージのインストール
時系列予測用の環境を設定するために、最初にlocal programming environmentまたはserver-based programming environmentに移動しましょう。
cd environments. my_env/bin/activateここから、プロジェクト用の新しいディレクトリを作成しましょう。 これをARIMAと呼び、ディレクトリに移動します。 プロジェクトを別の名前で呼ぶ場合は、ガイド全体で必ずARIMAの代わりに自分の名前を使用してください
mkdir ARIMA
cd ARIMAこのチュートリアルでは、warnings、itertools、pandas、numpy、matplotlib、およびstatsmodelsライブラリが必要です。 warningsおよびitertoolsライブラリは標準のPythonライブラリセットに含まれているため、インストールする必要はありません。
他のPythonパッケージと同様に、これらの要件をpip。
でインストールできます。pandas、statsmodels、およびデータプロットパッケージmatplotlibをインストールできるようになりました。 それらの依存関係もインストールされます。
pip install pandas numpy statsmodels matplotlibこの時点で、インストールされたパッケージの操作を開始するように設定されました。
[[step-2 -—- importing-packages-and-loading-data]] ==ステップ2—パッケージのインポートとデータのロード
データの操作を開始するには、Jupyter Notebookを起動します。
jupyter notebook新しいノートブックファイルを作成するには、右上のプルダウンメニューからNew>Python 3を選択します。
これにより、ノートブックが開きます。
ベストプラクティスとして、ノートブックの上部に必要なimporting the librariesから始めます。
import warnings
import itertools
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')また、プロットのmatplotlib styleをファイブサーティエイトと定義しました。
1958年3月から2001年12月にかけてCO2サンプルを収集した「米国ハワイ州マウナロア天文台の大気サンプルからの大気CO2」というデータセットを使用します。 このデータを次のように取り込むことができます。
data = sm.datasets.co2.load_pandas()
y = data.data先に進む前に、データを少し前処理しましょう。 週単位のデータは時間が短いため、取り扱いが難しい場合があります。代わりに月単位の平均を使用してみましょう。 resample関数を使用して変換を行います。 簡単にするために、fillna() functionを使用して、時系列に欠落値がないことを確認することもできます。
# The 'MS' string groups the data in buckets by start of the month
y = y['co2'].resample('MS').mean()
# The term bfill means that we use the value before filling in missing values
y = y.fillna(y.bfill())
print(y)Outputco2
1958-03-01 316.100000
1958-04-01 317.200000
1958-05-01 317.433333
...
2001-11-01 369.375000
2001-12-01 371.020000データの視覚化としてこの時系列eを調べてみましょう。
y.plot(figsize=(15, 6))
plt.show()
データをプロットすると、いくつかの識別可能なパターンが表示されます。 時系列には明らかな季節性パターンがあり、全体的に増加傾向にあります。
時系列の前処理の詳細については、「https://www.digitalocean.com/community/tutorials/a-guide-to-time-series-visualization-with-python-3 [時間ガイド上記のステップがより詳細に説明されています。
データを変換して調査したので、ARIMAを使用した時系列予測に進みましょう。
[[step-3 -—- the-arima-time-series-model]] ==ステップ3—ARIMA時系列モデル
時系列予測で使用される最も一般的な方法の1つは、ARIMAモデルとして知られています。これは、AutoregRessiveIntegratedMovingAverageを表します。 ARIMAは、時系列の将来のポイントをよりよく理解または予測するために、時系列データに適合できるモデルです。
ARIMAモデルをパラメーター化するために使用される3つの異なる整数(p、d、q)があります。 そのため、ARIMAモデルはARIMA(p, d, q)という表記で表されます。 これら3つのパラメーターを合わせて、データセットの季節性、傾向、およびノイズを説明します。
-
pは、モデルのauto-regressive部分です。 これにより、過去の値の効果をモデルに組み込むことができます。 直観的には、これは過去3日間暖かかった場合、明日は暖かくなる可能性が高いと述べることに似ています。 -
dは、モデルのintegrated部分です。 これには、差分の量を組み込むモデルの用語が含まれます(つまり、 時系列に適用するために、現在の値から減算する過去の時点の数)。 直観的には、これは、過去3日間の気温の差が非常に小さい場合、明日は同じ気温になる可能性が高いと述べることに似ています。 -
qは、モデルのmoving average部分です。 これにより、過去の過去の時点で観測されたエラー値の線形結合としてモデルのエラーを設定できます。
季節的な影響を扱うときは、ARIMA(p,d,q)(P,D,Q)sで表されるseasonalARIMAを使用します。 ここで、(p, d, q)は上記の非季節パラメータですが、(P, D, Q)は同じ定義に従いますが、時系列の季節コンポーネントに適用されます。 sという用語は、時系列の周期性です(四半期の期間の場合は4、年次の期間の場合は12など)。
季節のARIMAメソッドは、複数のチューニングパラメーターが関係しているため、気が遠くなる可能性があります。 次のセクションでは、季節的なARIMA時系列モデルの最適なパラメーターセットを識別するプロセスを自動化する方法について説明します。
[[step-4 -—- arima-time-series-modelのパラメーター選択]] ==ステップ4—ARIMA時系列モデルのパラメーター選択
時系列データを季節ARIMAモデルに適合させることを検討する場合、最初の目標は、対象のメトリックを最適化するARIMA(p,d,q)(P,D,Q)sの値を見つけることです。 この目標を達成するための多くのガイドラインとベストプラクティスがありますが、ARIMAモデルの正しいパラメーター化は、ドメインの専門知識と時間を必要とする骨の折れる手動プロセスになる可能性があります。 Rなどの他の統計プログラミング言語はautomated ways to solve this issueを提供しますが、それらはまだPythonに移植されていません。 このセクションでは、ARIMA(p,d,q)(P,D,Q)s時系列モデルに最適なパラメーター値をプログラムで選択するPythonコードを記述して、この問題を解決します。
「グリッド検索」を使用して、パラメーターのさまざまな組み合わせを繰り返し探索します。 パラメータの組み合わせごとに、新しい季節ARIMAモデルをstatsmodelsモジュールのSARIMAX()関数に適合させ、その全体的な品質を評価します。 パラメータの全体像を調べた後、最適なパラメータのセットが、関心のある基準に対して最高のパフォーマンスをもたらすものになります。 評価するパラメータのさまざまな組み合わせを生成することから始めましょう。
# Define the p, d and q parameters to take any value between 0 and 2
p = d = q = range(0, 2)
# Generate all different combinations of p, q and q triplets
pdq = list(itertools.product(p, d, q))
# Generate all different combinations of seasonal p, q and q triplets
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
print('Examples of parameter combinations for Seasonal ARIMA...')
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[1]))
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[2]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[3]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[4]))OutputExamples of parameter combinations for Seasonal ARIMA...
SARIMAX: (0, 0, 1) x (0, 0, 1, 12)
SARIMAX: (0, 0, 1) x (0, 1, 0, 12)
SARIMAX: (0, 1, 0) x (0, 1, 1, 12)
SARIMAX: (0, 1, 0) x (1, 0, 0, 12)上記で定義したパラメーターのトリプレットを使用して、さまざまな組み合わせでARIMAモデルをトレーニングおよび評価するプロセスを自動化できます。 Statistics and Machine Learningでは、このプロセスはモデル選択のグリッド検索(またはハイパーパラメーター最適化)として知られています。
さまざまなパラメーターに適合した統計モデルを評価および比較する場合、データに適合しているか、または将来のデータポイントを正確に予測する能力に基づいて、それぞれをランク付けできます。 AIC(赤池情報量基準)値を使用します。これは、statsmodelsを使用して適合されたARIMAモデルで便利に返されます。 AICは、モデルの全体的な複雑さを考慮しながら、モデルがデータにどの程度適合しているかを測定します。 多くの特徴を使用しながらデータに非常によく適合するモデルには、同じ適合度を達成するために少ない特徴を使用するモデルよりも大きなAICスコアが割り当てられます。 したがって、AICの値が最も低くなるモデルを見つけることに関心があります。
以下のコードチャンクは、パラメーターの組み合わせを反復処理し、statsmodelsのSARIMAX関数を使用して、対応する季節ARIMAモデルに適合させます。 ここで、order引数は(p, d, q)パラメーターを指定し、seasonal_order引数は季節ARIMAモデルの(P, D, Q, S)季節成分を指定します。 各SARIMAX()+`model, the code prints out its respective `+AICスコアをフィッティングした後。
warnings.filterwarnings("ignore") # specify to ignore warning messages
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(y,
order=param,
seasonal_order=param_seasonal,
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print('ARIMA{}x{}12 - AIC:{}'.format(param, param_seasonal, results.aic))
except:
continueパラメーターの組み合わせによっては数値の指定ミスを引き起こす可能性があるため、警告メッセージの過負荷を避けるために、警告メッセージを明示的に無効にしました。 これらの誤った仕様もエラーにつながり、例外をスローする可能性があるため、これらの例外をキャッチし、これらの問題を引き起こすパラメーターの組み合わせを無視するようにします。
上記のコードでは次の結果が得られます。これには時間がかかる場合があります。
OutputSARIMAX(0, 0, 0)x(0, 0, 1, 12) - AIC:6787.3436240402125
SARIMAX(0, 0, 0)x(0, 1, 1, 12) - AIC:1596.711172764114
SARIMAX(0, 0, 0)x(1, 0, 0, 12) - AIC:1058.9388921320026
SARIMAX(0, 0, 0)x(1, 0, 1, 12) - AIC:1056.2878315690562
SARIMAX(0, 0, 0)x(1, 1, 0, 12) - AIC:1361.6578978064144
SARIMAX(0, 0, 0)x(1, 1, 1, 12) - AIC:1044.7647912940095
...
...
...
SARIMAX(1, 1, 1)x(1, 0, 0, 12) - AIC:576.8647112294245
SARIMAX(1, 1, 1)x(1, 0, 1, 12) - AIC:327.9049123596742
SARIMAX(1, 1, 1)x(1, 1, 0, 12) - AIC:444.12436865161305
SARIMAX(1, 1, 1)x(1, 1, 1, 12) - AIC:277.7801413828764コードの出力は、SARIMAX(1, 1, 1)x(1, 1, 1, 12)が最低のAIC値277.78を生成することを示しています。 したがって、これは検討したすべてのモデルの中で最適なオプションであると考えるべきです。
[[step-5 --- fitting-an-arima-time-series-model]] ==ステップ5—ARIMA時系列モデルのフィッティング
グリッド検索を使用して、時系列データに最適なモデルを生成する一連のパラメーターを特定しました。 この特定のモデルをさらに詳しく分析することができます。
まず、最適なパラメータ値を新しいSARIMAXモデルにプラグインします。
mod = sm.tsa.statespace.SARIMAX(y,
order=(1, 1, 1),
seasonal_order=(1, 1, 1, 12),
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print(results.summary().tables[1])Output==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.3182 0.092 3.443 0.001 0.137 0.499
ma.L1 -0.6255 0.077 -8.165 0.000 -0.776 -0.475
ar.S.L12 0.0010 0.001 1.732 0.083 -0.000 0.002
ma.S.L12 -0.8769 0.026 -33.811 0.000 -0.928 -0.826
sigma2 0.0972 0.004 22.634 0.000 0.089 0.106
==============================================================================SARIMAXの出力から得られるsummary属性は、かなりの量の情報を返しますが、係数の表に注目します。 coef列は、重みを示します(つまり、 重要度)および各機能が時系列に与える影響。 P>|z|列は、各特徴の重みの重要性を通知します。 ここで、各重みのp値は0.05よりも低いか近いため、モデルにすべてを保持するのが妥当です。
季節性ARIMAモデル(およびその他のモデル)をフィッティングする場合、モデル診断を実行して、モデルによって行われた仮定に違反していないことを確認することが重要です。 plot_diagnosticsオブジェクトを使用すると、モデル診断をすばやく生成し、異常な動作を調査できます。
results.plot_diagnostics(figsize=(15, 12))
plt.show()
私たちの主な関心事は、モデルの残差が無相関で、平均ゼロで正規分布することを保証することです。 季節性ARIMAモデルがこれらの特性を満たさない場合、さらに改善できることを示す良い兆候です。
この場合、モデル診断により、モデルの残差は次のことに基づいて正規分布することが示唆されます。
-
右上のプロットでは、赤い
KDE線がN(0,1)線(N(0,1))が平均0の正規分布の標準表記であることがわかります。および1の標準偏差)。 これは、残差が正規分布していることを示しています。 -
左下のqq-plotは、残差(青い点)の順序付けられた分布が、
N(0, 1)の標準正規分布から取得されたサンプルの線形傾向に従うことを示しています。 繰り返しますが、これは残差が正規分布していることを強く示しています。 -
経時的な残差(左上のプロット)は明らかな季節性を示さず、ホワイトノイズのように見えます。 これは自己相関によって確認されます(つまり、 correlogram)は、右下のプロットであり、時系列残差はそれ自体の時間差バージョンとの相関が低いことを示しています。
これらの観察から、モデルは時系列データを理解し、将来の値を予測するのに役立つ満足のいく近似を生成すると結論付けることができます。
十分な適合がありますが、季節のARIMAモデルの一部のパラメーターを変更して、モデルの適合を改善することができます。 たとえば、グリッド検索ではパラメーターの組み合わせの制限されたセットのみが考慮されているため、グリッド検索を広げるとより良いモデルが見つかる場合があります。
[[step-6 -—- validating-forecasts]] ==ステップ6—予測の検証
時系列のモデルを取得し、これを使用して予測を作成できます。 予測値を時系列の実際の値と比較することから始めます。これは、予測の精度を理解するのに役立ちます。 get_prediction()属性とconf_int()属性を使用すると、時系列の予測の値と関連する信頼区間を取得できます。
pred = results.get_prediction(start=pd.to_datetime('1998-01-01'), dynamic=False)
pred_ci = pred.conf_int()上記のコードでは、1998年1月に予測を開始する必要があります。
dynamic=False引数は、一歩先の予測を生成することを保証します。つまり、各ポイントの予測は、そのポイントまでの完全な履歴を使用して生成されます。
CO2時系列の実際の値と予測値をプロットして、どの程度うまくいったかを評価できます。 日付インデックスをスライスすることで、時系列の終わりにズームインしたことに注目してください。
ax = y['1990':].plot(label='observed')
pred.predicted_mean.plot(ax=ax, label='One-step ahead Forecast', alpha=.7)
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.2)
ax.set_xlabel('Date')
ax.set_ylabel('CO2 Levels')
plt.legend()
plt.show()
全体として、予測は真の値と非常によく一致しており、全体的な増加傾向を示しています。
予測の精度を定量化することも役立ちます。 予測の平均誤差を要約するMSE(平均二乗誤差)を使用します。 各予測値について、真の値までの距離を計算し、結果を二乗します。 全体の平均を計算するときに正/負の差が互いに相殺されないように、結果を二乗する必要があります。
y_forecasted = pred.predicted_mean
y_truth = y['1998-01-01':]
# Compute the mean square error
mse = ((y_forecasted - y_truth) ** 2).mean()
print('The Mean Squared Error of our forecasts is {}'.format(round(mse, 2)))OutputThe Mean Squared Error of our forecasts is 0.07一歩先の予測のMSEは、0.07の値を生成します。これは、0に近いため、非常に低くなります。 MSEが0の場合、推定器はパラメーターの観測値を完全な精度で予測します。これは理想的なシナリオですが、通常は不可能です。
ただし、動的予測を使用すると、真の予測力をより適切に表現できます。 この場合、特定の時点までの時系列からの情報のみを使用し、その後、以前の予測された時点からの値を使用して予測が生成されます。
以下のコードチャンクでは、1998年1月以降の動的予測と信頼区間の計算を開始するように指定しています。
pred_dynamic = results.get_prediction(start=pd.to_datetime('1998-01-01'), dynamic=True, full_results=True)
pred_dynamic_ci = pred_dynamic.conf_int()時系列の観測値と予測値をプロットすると、動的予測を使用している場合でも全体的な予測が正確であることがわかります。 すべての予測値(赤線)はグラウンドトゥルース(青線)にほぼ一致しており、予測の信頼区間内に十分収まっています。
ax = y['1990':].plot(label='observed', figsize=(20, 15))
pred_dynamic.predicted_mean.plot(label='Dynamic Forecast', ax=ax)
ax.fill_between(pred_dynamic_ci.index,
pred_dynamic_ci.iloc[:, 0],
pred_dynamic_ci.iloc[:, 1], color='k', alpha=.25)
ax.fill_betweenx(ax.get_ylim(), pd.to_datetime('1998-01-01'), y.index[-1],
alpha=.1, zorder=-1)
ax.set_xlabel('Date')
ax.set_ylabel('CO2 Levels')
plt.legend()
plt.show()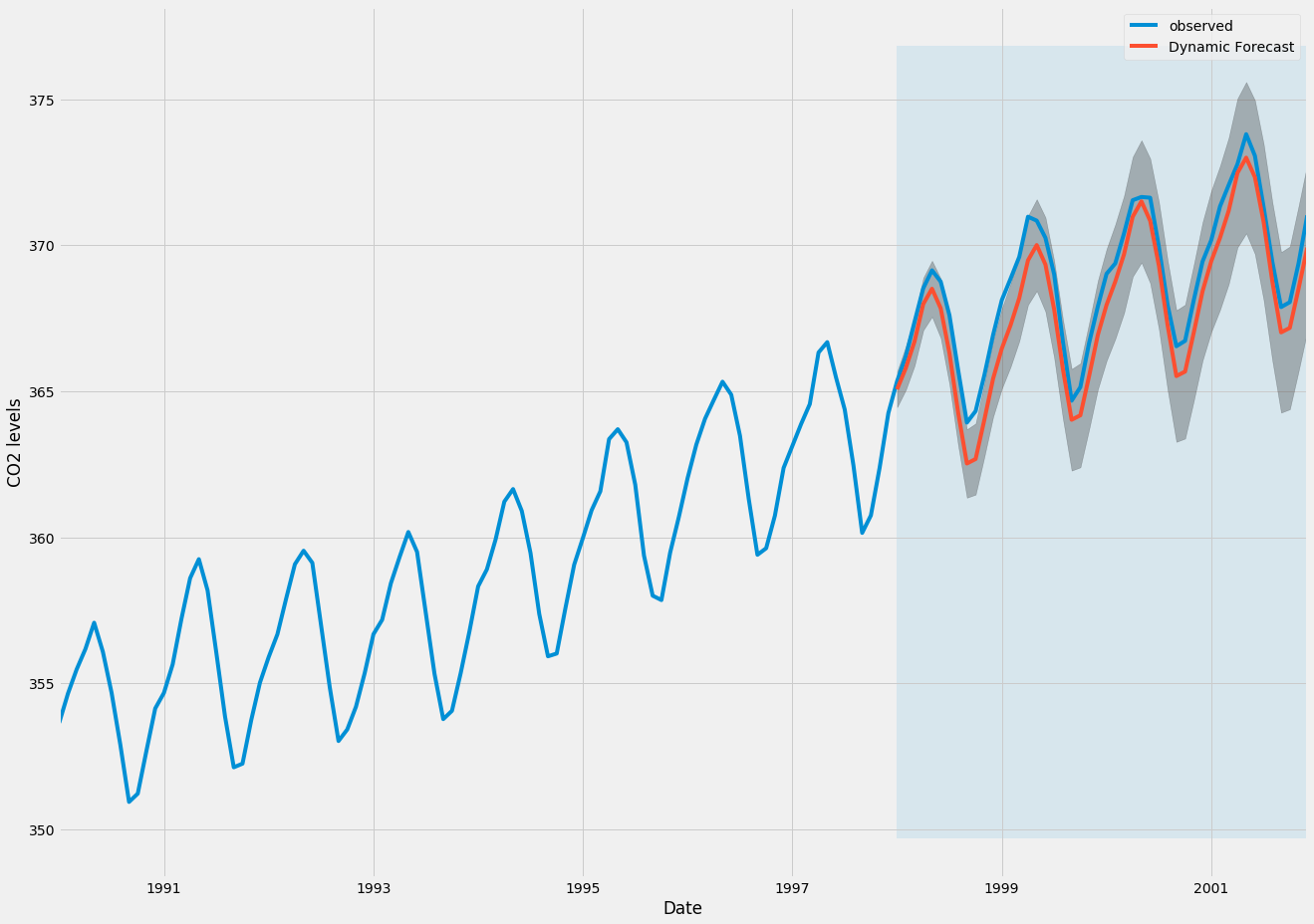
ここでも、MSEを計算することにより、予測の予測パフォーマンスを定量化します。
# Extract the predicted and true values of our time series
y_forecasted = pred_dynamic.predicted_mean
y_truth = y['1998-01-01':]
# Compute the mean square error
mse = ((y_forecasted - y_truth) ** 2).mean()
print('The Mean Squared Error of our forecasts is {}'.format(round(mse, 2)))OutputThe Mean Squared Error of our forecasts is 1.01動的予測から得られた予測値のMSEは1.01です。 これは、時系列からの履歴データが少ないことに依存していることを考えると、1つ先のステップよりもわずかに高くなります。
一歩先の予測と動的予測の両方により、この時系列モデルが有効であることが確認されます。 ただし、時系列予測に関する関心の多くは、将来の値を前もって予測する機能です。
[[step-7 -—- produce-and-visualizing-forecasts]] ==ステップ7—予測の作成と視覚化
このチュートリアルの最後のステップでは、季節のARIMA時系列モデルを活用して将来の値を予測する方法について説明します。 時系列オブジェクトのget_forecast()属性は、指定されたステップ数先の予測値を計算できます。
# Get forecast 500 steps ahead in future
pred_uc = results.get_forecast(steps=500)
# Get confidence intervals of forecasts
pred_ci = pred_uc.conf_int()このコードの出力を使用して、時系列と将来値の予測をプロットできます。
ax = y.plot(label='observed', figsize=(20, 15))
pred_uc.predicted_mean.plot(ax=ax, label='Forecast')
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.25)
ax.set_xlabel('Date')
ax.set_ylabel('CO2 Levels')
plt.legend()
plt.show()
生成した予測と関連する信頼区間の両方を使用して、時系列をさらに理解し、予想される内容を予測できるようになりました。 私たちの予測は、時系列が安定したペースで増加し続けると予想されることを示しています。
将来に向かってさらに予測すると、私たちの価値に自信がなくなるのは自然なことです。 これは、モデルによって生成された信頼区間に反映されます。信頼区間は、将来に進むにつれて大きくなります。
結論
このチュートリアルでは、Pythonで季節限定ARIMAモデルを実装する方法について説明しました。 pandasおよびstatsmodelsライブラリを広範囲に使用し、モデル診断を実行する方法と、CO2時系列の予測を作成する方法を示しました。
他にも試すことができるものがいくつかあります。
-
動的予測の開始日を変更して、予測の全体的な品質にどのように影響するかを確認します。
-
パラメーターの組み合わせをさらに試して、モデルの適合度を改善できるかどうかを確認してください。
-
別のメトリックを選択して、最適なモデルを選択します。 たとえば、
AICメジャーを使用して最適なモデルを見つけましたが、代わりにサンプル外の平均二乗誤差を最適化することもできます。
さらに練習するために、別の時系列データセットを読み込んで、独自の予測を作成することもできます。