introduction
Les séries chronologiques permettent de prévoir les valeurs futures. Sur la base des valeurs précédentes, des séries chronologiques peuvent être utilisées pour prévoir les tendances en matière d'économie, de météo et de planification de la capacité, pour n'en nommer que quelques-unes. Les propriétés spécifiques des données chronologiques font que des méthodes statistiques spécialisées sont généralement nécessaires.
Dans ce tutoriel, nous viserons à produire des prévisions fiables de séries chronologiques. Nous commencerons par présenter et discuter les concepts d'autocorrélation, de stationnarité et de saisonnalité, puis d'appliquer l'une des méthodes les plus couramment utilisées pour la prévision de séries chronologiques, ARIMA.
L'une des méthodes disponibles en Python pour modéliser et prédire les points futurs d'une série chronologique est connue sous le nom deSARIMAX, qui signifieSeasonal AutoRegressive Integrated Moving Averages with eXogenous regressors. Ici, nous nous concentrerons principalement sur la composante ARIMA, qui est utilisée pour ajuster les données de séries chronologiques afin de mieux comprendre et prévoir les points futurs de la série chronologique.
Conditions préalables
Ce guide explique comment effectuer des analyses chronologiques sur un poste de travail local ou un serveur distant. Travailler avec de grands ensembles de données peut demander beaucoup de mémoire, donc dans les deux cas, l'ordinateur aura besoin d'au moins2GB of memory pour effectuer certains des calculs de ce guide.
Pour tirer le meilleur parti de ce didacticiel, une connaissance des séries chronologiques et des statistiques peut être utile.
Pour ce didacticiel, nous utiliseronsJupyter Notebook pour travailler avec les données. Si vous ne l'avez pas déjà, vous devriez suivre nostutorial to install and set up Jupyter Notebook for Python 3.
[[step-1 -—- Installing-packages]] == Étape 1 - Installation des packages
Pour configurer notre environnement pour les prévisions de séries chronologiques, passons d'abord à noslocal programming environment ouserver-based programming environment:
cd environments. my_env/bin/activateÀ partir de là, créons un nouveau répertoire pour notre projet. Nous l'appelleronsARIMA puis nous nous déplacerons dans le répertoire. Si vous appelez le projet un nom différent, assurez-vous de remplacer votre nom parARIMA tout au long du guide
mkdir ARIMA
cd ARIMACe didacticiel nécessitera les bibliothèqueswarnings,itertools,pandas,numpy,matplotlib etstatsmodels. Les bibliothèqueswarnings etitertools sont fournies avec l'ensemble de bibliothèques Python standard, vous ne devriez donc pas avoir besoin de les installer.
Comme avec les autres packages Python, nous pouvons installer ces exigences avecpip.
Nous pouvons maintenant installerpandas,statsmodels et le package de traçage de donnéesmatplotlib. Leurs dépendances seront également installées:
pip install pandas numpy statsmodels matplotlibÀ ce stade, nous sommes maintenant configurés pour commencer à utiliser les packages installés.
[[step-2 -—- importing-packages-and-loading-data]] == Étape 2 - Importation de packages et chargement de données
Pour commencer à utiliser nos données, nous allons démarrer Jupyter Notebook:
jupyter notebookPour créer un nouveau fichier notebook, sélectionnezNew>Python 3 dans le menu déroulant en haut à droite:
Cela ouvrira un cahier.
Selon la meilleure pratique, commencez parimporting the libraries dont vous aurez besoin en haut de votre bloc-notes:
import warnings
import itertools
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')Nous avons également défini unmatplotlib style de cinq trente-huit pour nos parcelles.
Nous allons travailler avec un ensemble de données appelé «CO2 atmosphérique provenant d’échantillons d’air continus à l’observatoire du Mauna Loa, Hawaii, États-Unis», qui a recueilli des échantillons de CO2 de mars 1958 à décembre 2001. Nous pouvons apporter ces données comme suit:
data = sm.datasets.co2.load_pandas()
y = data.dataPrétraitons un peu nos données avant d’aller de l’avant. Les données hebdomadaires peuvent être délicates à utiliser car leur temps est plus court, alors utilisons plutôt les moyennes mensuelles. Nous allons faire la conversion avec la fonctionresample. Pour plus de simplicité, nous pouvons également utiliser lesfillna() function pour nous assurer que nous n'avons aucune valeur manquante dans notre série chronologique.
# The 'MS' string groups the data in buckets by start of the month
y = y['co2'].resample('MS').mean()
# The term bfill means that we use the value before filling in missing values
y = y.fillna(y.bfill())
print(y)Outputco2
1958-03-01 316.100000
1958-04-01 317.200000
1958-05-01 317.433333
...
2001-11-01 369.375000
2001-12-01 371.020000Explorons cette série chronologique en tant que visualisation de données:
y.plot(figsize=(15, 6))
plt.show()
Certains modèles distincts apparaissent lorsque nous traçons les données. La série chronologique présente une tendance saisonnière évidente, ainsi qu'une tendance générale à la hausse.
Pour en savoir plus sur le prétraitement des séries chronologiques, reportez-vous à la section «https://www.digitalocean.com/community/tutorials/a-guide-to-time-series-visualization-with-python-3[A Guide to Time Visualisation en série avec Python 3], ”, où les étapes ci-dessus sont décrites plus en détail.
Maintenant que nous avons converti et exploré nos données, passons à la prévision de séries chronologiques avec ARIMA.
[[step-3 -—- the-arima-time-series-model]] == Étape 3 - Le modèle de séries temporelles ARIMA
L'une des méthodes les plus courantes utilisées dans la prévision des séries chronologiques est le modèle ARIMA, qui signifieAutoregRessiveIntegratedMovingAverage. ARIMA est un modèle qui peut être ajusté aux données de séries chronologiques afin de mieux comprendre ou prévoir les points futurs de la série.
Il existe trois entiers distincts (p,d,q) qui sont utilisés pour paramétrer les modèles ARIMA. Pour cette raison, les modèles ARIMA sont désignés par la notationARIMA(p, d, q). Ensemble, ces trois paramètres prennent en compte la saisonnalité, la tendance et le bruit dans les jeux de données:
-
pest la partieauto-regressive du modèle. Cela nous permet d'intégrer l'effet des valeurs passées dans notre modèle. Intuitivement, cela reviendrait à dire qu’il fera probablement chaud demain si les 3 derniers jours ont été chauds. -
dest la partieintegrated du modèle. Ceci inclut les termes du modèle qui incorporent l’importance de la différenciation (c.-à-d. le nombre de points temporels passés à soustraire de la valeur actuelle) à appliquer à la série temporelle. Intuitivement, cela reviendrait à affirmer que ce sera probablement la même température demain si la différence de température au cours des trois derniers jours a été très faible. -
qest la partiemoving average du modèle. Cela nous permet de définir l'erreur de notre modèle comme une combinaison linéaire des valeurs d'erreur observées à des instants précédents dans le passé.
En ce qui concerne les effets saisonniers, nous utilisons leseasonal ARIMA, qui est notéARIMA(p,d,q)(P,D,Q)s. Ici,(p, d, q) sont les paramètres non saisonniers décrits ci-dessus, tandis que(P, D, Q) suivent la même définition mais sont appliqués à la composante saisonnière de la série chronologique. Le termes est la périodicité de la série chronologique (4 pour les périodes trimestrielles,12 pour les périodes annuelles, etc.).
La méthode ARIMA saisonnière peut sembler décourageante en raison des multiples paramètres de réglage impliqués. Dans la section suivante, nous allons décrire comment automatiser le processus d'identification du jeu de paramètres optimal pour le modèle de série chronologique ARIMA saisonnier.
[[step-4 -—- parameter-selection-for-the-arima-time-series-model]] == Étape 4 - Sélection des paramètres pour le modèle de série temporelle ARIMA
Lorsque vous cherchez à ajuster des données de séries chronologiques avec un modèle ARIMA saisonnier, notre premier objectif est de trouver les valeurs deARIMA(p,d,q)(P,D,Q)s qui optimisent une métrique d'intérêt. Il existe de nombreuses directives et meilleures pratiques pour atteindre cet objectif, mais la paramétrisation correcte des modèles ARIMA peut être un processus manuel fastidieux qui requiert une expertise et du temps du domaine. D'autres langages de programmation statistique tels queR fournissent desautomated ways to solve this issue, mais ceux-ci n'ont pas encore été portés vers Python. Dans cette section, nous allons résoudre ce problème en écrivant du code Python pour sélectionner par programme les valeurs de paramètre optimales pour notre modèle de série chronologiqueARIMA(p,d,q)(P,D,Q)s.
Nous allons utiliser une «recherche de grille» pour explorer de manière itérative différentes combinaisons de paramètres. Pour chaque combinaison de paramètres, nous ajustons un nouveau modèle ARIMA saisonnier avec la fonctionSARIMAX() du modulestatsmodels et évaluons sa qualité globale. Une fois que nous avons exploré tout le paysage des paramètres, notre ensemble optimal de paramètres sera celui qui donnera les meilleures performances pour nos critères d’intérêt. Commençons par générer les différentes combinaisons de paramètres que nous souhaitons évaluer:
# Define the p, d and q parameters to take any value between 0 and 2
p = d = q = range(0, 2)
# Generate all different combinations of p, q and q triplets
pdq = list(itertools.product(p, d, q))
# Generate all different combinations of seasonal p, q and q triplets
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
print('Examples of parameter combinations for Seasonal ARIMA...')
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[1]))
print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[2]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[3]))
print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[4]))OutputExamples of parameter combinations for Seasonal ARIMA...
SARIMAX: (0, 0, 1) x (0, 0, 1, 12)
SARIMAX: (0, 0, 1) x (0, 1, 0, 12)
SARIMAX: (0, 1, 0) x (0, 1, 1, 12)
SARIMAX: (0, 1, 0) x (1, 0, 0, 12)Nous pouvons maintenant utiliser les triplets de paramètres définis ci-dessus pour automatiser le processus de formation et d'évaluation des modèles ARIMA sur différentes combinaisons. Dans Statistics and Machine Learning, ce processus est appelé recherche de grille (ou optimisation d'hyperparamètre) pour la sélection de modèle.
Lors de l'évaluation et de la comparaison de modèles statistiques dotés de paramètres différents, chacun peut être comparé en fonction de son adéquation aux données ou de sa capacité à prédire avec précision les points de données futurs. Nous utiliserons la valeurAIC (Akaike Information Criterion), qui est commodément renvoyée avec les modèles ARIMA ajustés à l'aide destatsmodels. LeAIC mesure l'adéquation d'un modèle aux données tout en tenant compte de la complexité globale du modèle. Un modèle qui correspond très bien aux données tout en utilisant de nombreuses fonctionnalités se verra attribuer un score AIC plus élevé qu'un modèle qui utilise moins de fonctionnalités pour obtenir le même ajustement. Par conséquent, nous sommes intéressés à trouver le modèle qui donne la valeur deAICla plus faible.
Le bloc de code ci-dessous itère à travers des combinaisons de paramètres et utilise la fonctionSARIMAX destatsmodels pour s'adapter au modèle ARIMA saisonnier correspondant. Ici, l'argumentorder spécifie les paramètres(p, d, q), tandis que l'argumentseasonal_order spécifie la composante saisonnière(P, D, Q, S) du modèle Seasonal ARIMA. Après ajustement de chaque score deSARIMAX()+`model, the code prints out its respective `+AIC.
warnings.filterwarnings("ignore") # specify to ignore warning messages
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(y,
order=param,
seasonal_order=param_seasonal,
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print('ARIMA{}x{}12 - AIC:{}'.format(param, param_seasonal, results.aic))
except:
continueCertaines combinaisons de paramètres pouvant conduire à des erreurs de spécification numériques, nous avons explicitement désactivé les messages d’avertissement afin d’éviter une surcharge des messages d’avertissement. Ces erreurs de spécification peuvent également conduire à des erreurs et générer une exception. Nous nous assurons donc de capturer ces exceptions et d'ignorer les combinaisons de paramètres à l'origine de ces problèmes.
Le code ci-dessus devrait donner les résultats suivants, cela peut prendre un certain temps:
OutputSARIMAX(0, 0, 0)x(0, 0, 1, 12) - AIC:6787.3436240402125
SARIMAX(0, 0, 0)x(0, 1, 1, 12) - AIC:1596.711172764114
SARIMAX(0, 0, 0)x(1, 0, 0, 12) - AIC:1058.9388921320026
SARIMAX(0, 0, 0)x(1, 0, 1, 12) - AIC:1056.2878315690562
SARIMAX(0, 0, 0)x(1, 1, 0, 12) - AIC:1361.6578978064144
SARIMAX(0, 0, 0)x(1, 1, 1, 12) - AIC:1044.7647912940095
...
...
...
SARIMAX(1, 1, 1)x(1, 0, 0, 12) - AIC:576.8647112294245
SARIMAX(1, 1, 1)x(1, 0, 1, 12) - AIC:327.9049123596742
SARIMAX(1, 1, 1)x(1, 1, 0, 12) - AIC:444.12436865161305
SARIMAX(1, 1, 1)x(1, 1, 1, 12) - AIC:277.7801413828764La sortie de notre code suggère queSARIMAX(1, 1, 1)x(1, 1, 1, 12) donne la valeurAIC la plus basse de 277,78. Nous devrions donc considérer cette option comme optimale parmi tous les modèles que nous avons examinés.
[[step-5 -—- fit-an-arima-time-series-model]] == Étape 5 - Ajuster un modèle de série temporelle ARIMA
En utilisant la recherche par grille, nous avons identifié le jeu de paramètres qui produit le modèle le mieux adapté à nos données chronologiques. Nous pouvons procéder à une analyse plus approfondie de ce modèle particulier.
Nous allons commencer par insérer les valeurs optimales des paramètres dans un nouveau modèleSARIMAX:
mod = sm.tsa.statespace.SARIMAX(y,
order=(1, 1, 1),
seasonal_order=(1, 1, 1, 12),
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print(results.summary().tables[1])Output==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.3182 0.092 3.443 0.001 0.137 0.499
ma.L1 -0.6255 0.077 -8.165 0.000 -0.776 -0.475
ar.S.L12 0.0010 0.001 1.732 0.083 -0.000 0.002
ma.S.L12 -0.8769 0.026 -33.811 0.000 -0.928 -0.826
sigma2 0.0972 0.004 22.634 0.000 0.089 0.106
==============================================================================L'attributsummary qui résulte de la sortie deSARIMAX renvoie une quantité importante d'informations, mais nous concentrerons notre attention sur le tableau des coefficients. La colonnecoef indique le poids (c.-à-d. importance) de chaque caractéristique et son impact sur la série chronologique. La colonneP>|z| nous informe de la signification de chaque poids de caractéristique. Ici, chaque poids a une valeur p inférieure ou proche de0.05, il est donc raisonnable de les conserver tous dans notre modèle.
Lors de l'ajustement des modèles ARIMA saisonniers (et de tout autre modèle), il est important d'exécuter des diagnostics de modèle pour s'assurer qu'aucune des hypothèses formulées par le modèle n'a été violée. L'objetplot_diagnostics nous permet de générer rapidement des diagnostics de modèle et de rechercher tout comportement inhabituel.
results.plot_diagnostics(figsize=(15, 12))
plt.show()
Notre principale préoccupation est de nous assurer que les résidus de notre modèle ne sont pas corrélés et sont normalement distribués avec une moyenne nulle. Si le modèle saisonnier ARIMA ne satisfait pas à ces propriétés, cela indique qu'il peut encore être amélioré.
Dans ce cas, nos diagnostics de modèle suggèrent que les résidus de modèle sont normalement répartis en fonction des éléments suivants:
-
Dans le graphique en haut à droite, nous voyons que la ligne rouge
KDEsuit de près la ligneN(0,1)(oùN(0,1)) est la notation standard pour une distribution normale avec une moyenne de0et écart type de1). C'est une bonne indication que les résidus sont normalement distribués. -
Leqq-plot en bas à gauche montre que la distribution ordonnée des résidus (points bleus) suit la tendance linéaire des échantillons prélevés à partir d'une distribution normale standard avec
N(0, 1). Là encore, cela indique clairement que les résidus sont normalement distribués. -
Les résidus dans le temps (graphique en haut à gauche) ne présentent aucune saisonnalité évidente et apparaissent comme un bruit blanc. Ceci est confirmé par l'autocorrélation (c'est-à-dire corrélogramme) en bas à droite, qui montre que les résidus de la série temporelle ont une faible corrélation avec les versions décalées de lui-même.
Ces observations nous amènent à conclure que notre modèle produit un ajustement satisfaisant qui pourrait nous aider à comprendre nos données de série chronologique et à prévoir nos valeurs futures.
Bien que notre ajustement soit satisfaisant, certains paramètres de notre modèle ARIMA saisonnier pourraient être modifiés pour améliorer cet ajustement. Par exemple, notre recherche dans la grille n'a pris en compte qu'un ensemble restreint de combinaisons de paramètres. Il est donc possible que nous trouvions de meilleurs modèles si nous élargissions la recherche dans la grille.
[[step-6 -—- validating-prévisions]] == Étape 6 - Validation des prévisions
Nous avons obtenu un modèle pour notre série chronologique qui peut maintenant être utilisé pour produire des prévisions. Nous commençons par comparer les valeurs prédites aux valeurs réelles de la série chronologique, ce qui nous aidera à comprendre la précision de nos prévisions. Les attributsget_prediction() etconf_int() nous permettent d'obtenir les valeurs et les intervalles de confiance associés pour les prévisions de la série chronologique.
pred = results.get_prediction(start=pd.to_datetime('1998-01-01'), dynamic=False)
pred_ci = pred.conf_int()Le code ci-dessus exige que les prévisions commencent en janvier 1998.
L'argumentdynamic=False garantit que nous produisons des prévisions avec une longueur d'avance, ce qui signifie que les prévisions à chaque point sont générées en utilisant l'historique complet jusqu'à ce point.
Nous pouvons tracer les valeurs réelles et prévues de la série chronologique sur le CO2 pour évaluer notre succès. Remarquez comment nous avons zoomé sur la fin de la série temporelle en découpant l’index de la date.
ax = y['1990':].plot(label='observed')
pred.predicted_mean.plot(ax=ax, label='One-step ahead Forecast', alpha=.7)
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.2)
ax.set_xlabel('Date')
ax.set_ylabel('CO2 Levels')
plt.legend()
plt.show()
Dans l’ensemble, nos prévisions s’alignent très bien sur les valeurs réelles, montrant une tendance générale à la hausse.
Il est également utile de quantifier la précision de nos prévisions. Nous utiliserons l’erreur MSE (Mean Squared Error), qui résume l’erreur moyenne de nos prévisions. Pour chaque valeur prédite, nous calculons sa distance à la valeur vraie et comparons le résultat. Les résultats doivent être cadrés pour que les différences positives / négatives ne s’annulent pas lorsque nous calculons la moyenne globale.
y_forecasted = pred.predicted_mean
y_truth = y['1998-01-01':]
# Compute the mean square error
mse = ((y_forecasted - y_truth) ** 2).mean()
print('The Mean Squared Error of our forecasts is {}'.format(round(mse, 2)))OutputThe Mean Squared Error of our forecasts is 0.07La MSE de nos prévisions à un pas en avant donne une valeur de0.07, ce qui est très faible car proche de 0. Une ESM de 0 indiquerait que l'estimateur prédit les observations du paramètre avec une précision parfaite, ce qui serait un scénario idéal mais qui n'est généralement pas possible.
Cependant, une meilleure représentation de notre véritable pouvoir prédictif peut être obtenue en utilisant des prévisions dynamiques. Dans ce cas, nous n'utilisons que les informations de la série chronologique jusqu'à un certain point. Par la suite, les prévisions sont générées à l'aide des valeurs des points de temps prévisionnels précédents.
Dans le bloc de code ci-dessous, nous spécifions de commencer à calculer les prévisions dynamiques et les intervalles de confiance à partir de janvier 1998.
pred_dynamic = results.get_prediction(start=pd.to_datetime('1998-01-01'), dynamic=True, full_results=True)
pred_dynamic_ci = pred_dynamic.conf_int()En traçant les valeurs observées et prévues de la série chronologique, nous constatons que les prévisions globales sont précises même lorsque vous utilisez des prévisions dynamiques. Toutes les valeurs prévues (ligne rouge) correspondent assez bien à la vérité au sol (ligne bleue) et se situent bien dans les intervalles de confiance de nos prévisions.
ax = y['1990':].plot(label='observed', figsize=(20, 15))
pred_dynamic.predicted_mean.plot(label='Dynamic Forecast', ax=ax)
ax.fill_between(pred_dynamic_ci.index,
pred_dynamic_ci.iloc[:, 0],
pred_dynamic_ci.iloc[:, 1], color='k', alpha=.25)
ax.fill_betweenx(ax.get_ylim(), pd.to_datetime('1998-01-01'), y.index[-1],
alpha=.1, zorder=-1)
ax.set_xlabel('Date')
ax.set_ylabel('CO2 Levels')
plt.legend()
plt.show()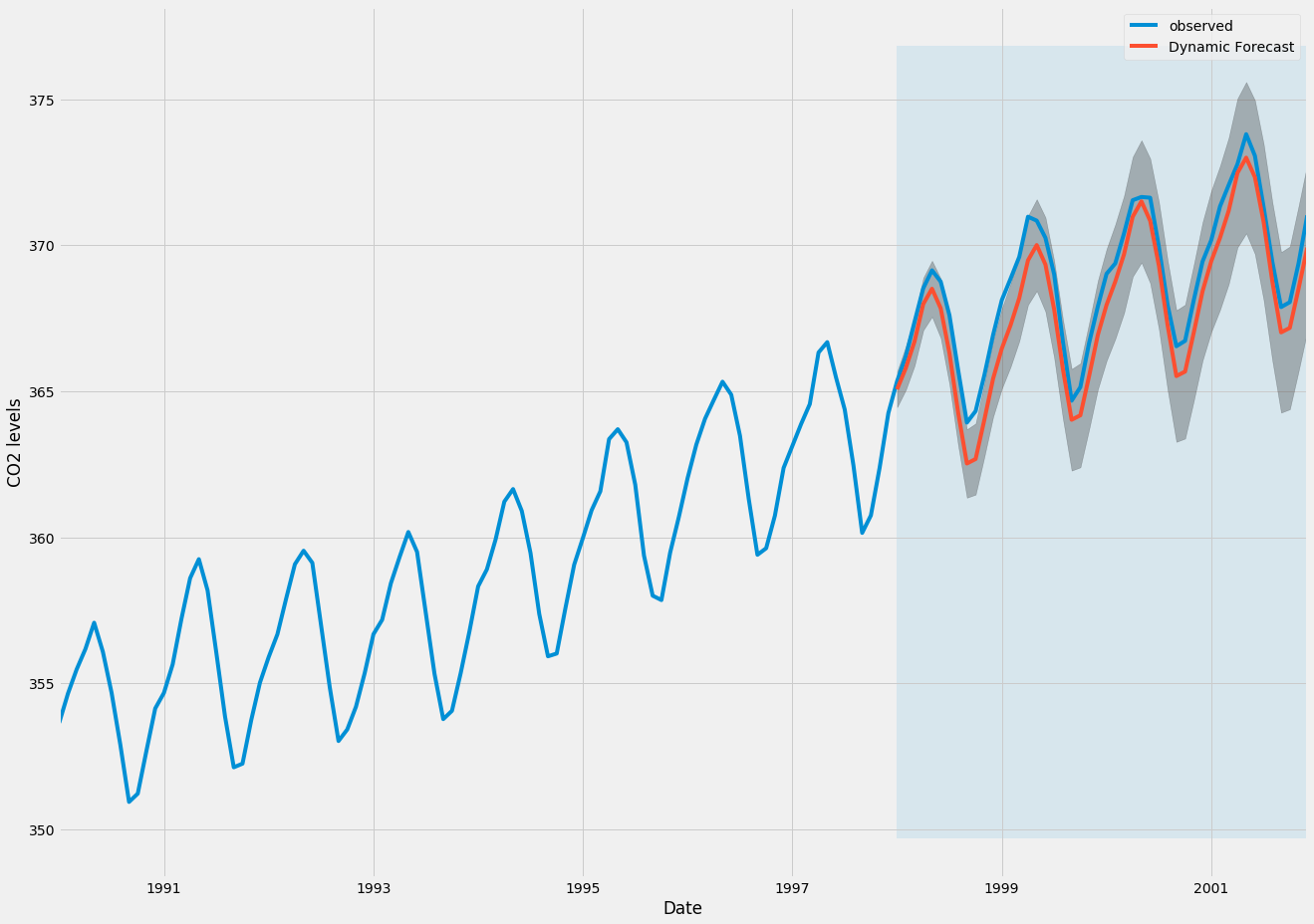
Une fois encore, nous quantifions la performance prédictive de nos prévisions en calculant le MSE:
# Extract the predicted and true values of our time series
y_forecasted = pred_dynamic.predicted_mean
y_truth = y['1998-01-01':]
# Compute the mean square error
mse = ((y_forecasted - y_truth) ** 2).mean()
print('The Mean Squared Error of our forecasts is {}'.format(round(mse, 2)))OutputThe Mean Squared Error of our forecasts is 1.01Les valeurs prédites obtenues à partir des prévisions dynamiques donnent une MSE de 1,01. Ce chiffre est légèrement supérieur au pas en avant attendu, compte tenu du fait que nous nous basons sur moins de données historiques issues de la série chronologique.
Les prévisions à une étape et les prévisions dynamiques confirment que ce modèle de série chronologique est valide. Cependant, l’intérêt pour la prévision de séries chronologiques réside dans la possibilité de prévoir les valeurs futures très longtemps dans le temps.
[[step-7 -—- production-and-visualizing-prévisions]] == Étape 7 - Production et visualisation des prévisions
Dans la dernière étape de ce didacticiel, nous décrivons comment utiliser notre modèle de série chronologique saisonnier ARIMA pour prévoir les valeurs futures. L'attributget_forecast() de notre objet de série chronologique peut calculer les valeurs prévues pour un nombre spécifié d'étapes à venir.
# Get forecast 500 steps ahead in future
pred_uc = results.get_forecast(steps=500)
# Get confidence intervals of forecasts
pred_ci = pred_uc.conf_int()Nous pouvons utiliser la sortie de ce code pour tracer la série chronologique et les prévisions de ses valeurs futures.
ax = y.plot(label='observed', figsize=(20, 15))
pred_uc.predicted_mean.plot(ax=ax, label='Forecast')
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.25)
ax.set_xlabel('Date')
ax.set_ylabel('CO2 Levels')
plt.legend()
plt.show()
Les prévisions et l’intervalle de confiance associé que nous avons générés peuvent maintenant être utilisés pour mieux comprendre la série chronologique et prévoir ce à quoi s’attendre. Nos prévisions indiquent que la série chronologique devrait continuer à augmenter à un rythme soutenu.
Alors que nous prévoyons plus loin dans l'avenir, il est naturel pour nous de perdre confiance en nos valeurs. Cela se reflète dans les intervalles de confiance générés par notre modèle, qui s’élargissent à mesure que nous progressons dans le futur.
Conclusion
Dans ce tutoriel, nous avons décrit comment implémenter un modèle ARIMA saisonnier en Python. Nous avons largement utilisé les bibliothèquespandas etstatsmodels et montré comment exécuter des diagnostics de modèle, ainsi que comment produire des prévisions de la série chronologique CO2.
Voici quelques autres choses que vous pourriez essayer:
-
Modifiez la date de début de vos prévisions dynamiques pour voir en quoi cela affecte la qualité globale de vos prévisions.
-
Essayez plusieurs combinaisons de paramètres pour voir si vous pouvez améliorer la qualité de l'ajustement de votre modèle.
-
Sélectionnez une métrique différente pour sélectionner le meilleur modèle. Par exemple, nous avons utilisé la mesure
AICpour trouver le meilleur modèle, mais vous pouvez plutôt chercher à optimiser l'erreur quadratique moyenne hors échantillon.
Pour plus de pratique, vous pouvez également essayer de charger un autre jeu de données de série chronologique pour produire vos propres prévisions.