Ein Leitfaden für die Vorhersage von Zeitreihen mit ARIMA in Python 3

Zeitreihen bieten die Möglichkeit, zukünftige Werte vorherzusagen. Basierend auf früheren Werten können Zeitreihen verwendet werden, um Trends in den Bereichen Wirtschaft, Wetter und Kapazitätsplanung vorherzusagen, um nur einige zu nennen. Aufgrund der spezifischen Eigenschaften von Zeitreihendaten sind in der Regel spezielle statistische Methoden erforderlich.

In diesem Tutorial wollen wir zuverlässige Prognosen für Zeitreihen erstellen. Wir werden zunächst die Konzepte von Autokorrelation, Stationarität und Saisonalität einführen und diskutieren und dann eine der am häufigsten verwendeten Methoden zur Vorhersage von Zeitreihen anwenden, die als ARIMA bezeichnet wird.

Eine der in Python verfügbaren Methoden zur Modellierung und Vorhersage zukünftiger Punkte einer Zeitreihe istSARIMAX, was fürSeasonal AutoRegressive Integrated Moving Averages with eXogenous regressors steht. Hier konzentrieren wir uns hauptsächlich auf die ARIMA-Komponente, mit der Zeitreihendaten angepasst werden, um zukünftige Punkte in der Zeitreihe besser zu verstehen und vorherzusagen.

In diesem Handbuch wird beschrieben, wie Sie Zeitreihen auf einem lokalen Desktop oder einem Remote-Server analysieren. Das Arbeiten mit großen Datenmengen kann speicherintensiv sein. In beiden Fällen benötigt der Computer mindestens2GB of memory, um einige der Berechnungen in diesem Handbuch durchzuführen.

Um dieses Lernprogramm optimal nutzen zu können, ist es hilfreich, sich mit Zeitreihen und Statistiken vertraut zu machen.

In diesem Tutorial verwenden wirJupyter Notebook, um mit den Daten zu arbeiten. Wenn Sie es noch nicht haben, sollten Sie unserentutorial to install and set up Jupyter Notebook for Python 3 folgen.

[[Schritt-1 - Installieren von Paketen]] == Schritt 1 - Installieren von Paketen

Um unsere Umgebung für die Vorhersage von Zeitreihen einzurichten, gehen wir zunächst zu unserenlocal programming environment oderserver-based programming environment über:

Erstellen wir von hier aus ein neues Verzeichnis für unser Projekt. Wir werden esARIMA nennen und dann in das Verzeichnis wechseln. Wenn Sie dem Projekt einen anderen Namen geben, müssen SieARIMA im gesamten Handbuch durch Ihren Namen ersetzen

Für dieses Lernprogramm sind die Bibliothekenwarnings,itertools,pandas,numpy,matplotlib undstatsmodelserforderlich. Die Bibliothekenwarnings unditertoolsind im Standard-Python-Bibliothekssatz enthalten, sodass Sie sie nicht installieren müssen.

Wie bei anderen Python-Paketen können wir diese Anforderungen mitpip.
installieren. Wir können jetztpandas,statsmodels und das Datenplot-Paketmatplotlib installieren. Ihre Abhängigkeiten werden ebenfalls installiert:

Jetzt können wir mit den installierten Paketen arbeiten.

[[Schritt 2 - Importieren von Paketen und Laden von Daten] == Schritt 2 - Importieren von Paketen und Laden von Daten

Um mit unseren Daten zu arbeiten, starten wir Jupyter Notebook:

Um eine neue Notebook-Datei zu erstellen, wählen Sie im Pulldown-Menü oben rechtsNew>Python 3 aus:

Dies öffnet ein Notizbuch.

Beginnen Sie wie empfohlen mitimporting the libraries, die Sie oben in Ihrem Notizbuch benötigen:

Wir haben auch einen Prozentsatz (t0) von fünfunddreißig für unsere Parzellen definiert.

Wir werden mit einem Datensatz namens "Atmosphärisches CO2 aus kontinuierlichen Luftproben am Mauna Loa Observatory, Hawaii, USA" arbeiten, der von März 1958 bis Dezember 2001 CO2-Proben sammelte. Wir können diese Daten wie folgt einbringen:

Lassen Sie uns unsere Daten ein wenig vorverarbeiten, bevor wir fortfahren. Es kann schwierig sein, mit wöchentlichen Daten zu arbeiten, da die Zeit dafür kürzer ist. Verwenden wir stattdessen die Monatsmittelwerte. Wir werden die Konvertierung mit der Funktionresampledurchführen. Der Einfachheit halber können wir auchfillna() function verwenden, um sicherzustellen, dass in unseren Zeitreihen keine Werte fehlen.

Untersuchen wir diese Zeitreihe e als Datenvisualisierung:

Einige unterscheidbare Muster erscheinen, wenn wir die Daten zeichnen. Die Zeitreihen weisen ein offensichtliches Saisonalitätsmuster sowie einen insgesamt zunehmenden Trend auf.

Weitere Informationen zur Vorverarbeitung von Zeitreihen finden Sie unter „https://www.digitalocean.com/community/tutorials/a-guide-to-time-series-visualization-with-python-3[A Guide to Time“ Serienvisualisierung mit Python 3] “, in der die obigen Schritte ausführlicher beschrieben werden.

Nachdem wir unsere Daten konvertiert und untersucht haben, fahren wir mit der Prognose von Zeitreihen mit ARIMA fort.

[[Schritt 3 - Das Arima-Zeitreihenmodell]] == Schritt 3 - Das ARIMA-Zeitreihenmodell

Eine der am häufigsten verwendeten Methoden bei der Vorhersage von Zeitreihen ist das ARIMA-Modell, das fürAutoregRessiveIntegratedMvingAverage steht. ARIMA ist ein Modell, das an Zeitreihendaten angepasst werden kann, um zukünftige Punkte in der Reihe besser zu verstehen oder vorherzusagen.

Es gibt drei verschiedene Ganzzahlen (p,d,q), die zur Parametrisierung von ARIMA-Modellen verwendet werden. Aus diesem Grund werden ARIMA-Modelle mit der NotationARIMA(p, d, q) bezeichnet. Zusammen berücksichtigen diese drei Parameter die Saisonalität, den Trend und das Rauschen in Datasets:

Beim Umgang mit saisonalen Effekten verwenden wir die ARIMAseasonal, die alsARIMA(p,d,q)(P,D,Q)s bezeichnet wird. Hier sind(p, d, q) die oben beschriebenen nicht-saisonalen Parameter, während(P, D, Q) der gleichen Definition folgen, jedoch auf die saisonale Komponente der Zeitreihe angewendet werden. Der Begriffs ist die Periodizität der Zeitreihen (4 für vierteljährliche Perioden,12 für jährliche Perioden usw.).

Die saisonale ARIMA-Methode kann aufgrund der Vielzahl der beteiligten Optimierungsparameter entmutigend wirken. Im nächsten Abschnitt wird beschrieben, wie der Prozess zur Ermittlung des optimalen Parametersatzes für das saisonale ARIMA-Zeitreihenmodell automatisiert wird.

[[Schritt-4 -—- Parameterauswahl-für-das-Arima-Zeitreihenmodell]] == Schritt 4 - Parameterauswahl für das ARIMA-Zeitreihenmodell

Bei der Anpassung von Zeitreihendaten an ein saisonales ARIMA-Modell besteht unser erstes Ziel darin, die Werte vonARIMA(p,d,q)(P,D,Q)szu ermitteln, die eine interessierende Metrik optimieren. Es gibt viele Richtlinien und Best Practices, um dieses Ziel zu erreichen. Die korrekte Parametrisierung von ARIMA-Modellen kann jedoch ein sorgfältiger manueller Prozess sein, der Fachwissen und Zeit erfordert. Andere statistische Programmiersprachen wieR bietenautomated ways to solve this issue, diese müssen jedoch noch auf Python portiert werden. In diesem Abschnitt beheben wir dieses Problem, indem wir Python-Code schreiben, um programmgesteuert die optimalen Parameterwerte für das Zeitreihenmodell vonARIMA(p,d,q)(P,D,Q)sauszuwählen.

Wir werden eine "Rastersuche" verwenden, um iterativ verschiedene Kombinationen von Parametern zu untersuchen. Für jede Kombination von Parametern passen wir ein neues saisonales ARIMA-Modell mit der FunktionSARIMAX()aus dem Modulstatsmodelsan und bewerten dessen Gesamtqualität. Sobald wir die gesamte Parameterlandschaft untersucht haben, wird unser optimaler Parametersatz derjenige sein, der die beste Leistung für unsere interessierenden Kriterien erbringt. Beginnen wir mit der Generierung der verschiedenen Parameterkombinationen, die wir bewerten möchten:

Wir können nun die oben definierten Tripletts von Parametern verwenden, um den Prozess des Trainings und der Bewertung von ARIMA-Modellen für verschiedene Kombinationen zu automatisieren. In Statistik und maschinellem Lernen wird dieser Prozess als Rastersuche (oder Hyperparameteroptimierung) für die Modellauswahl bezeichnet.

Bei der Auswertung und dem Vergleich statistischer Modelle, die mit unterschiedlichen Parametern ausgestattet sind, kann jedes anhand der Übereinstimmung mit den Daten oder der Fähigkeit, zukünftige Datenpunkte genau vorherzusagen, in eine Rangfolge gebracht werden. Wir werden den WertAIC (Akaike Information Criterion) verwenden, der bequem mit ARIMA-Modellen zurückgegeben wird, die mitstatsmodels ausgestattet sind. DerAIC misst, wie gut ein Modell zu den Daten passt, wobei die Gesamtkomplexität des Modells berücksichtigt wird. Einem Modell, das bei Verwendung vieler Features sehr gut zu den Daten passt, wird ein höherer AIC-Wert zugewiesen als einem Modell, das weniger Features verwendet, um die gleiche Anpassungsgüte zu erzielen. Daher sind wir daran interessiert, das Modell zu finden, das den niedrigstenAIC-Wert liefert.

Der folgende Codeblock durchläuft Kombinationen von Parametern und verwendet die FunktionSARIMAX vonstatsmodels, um das entsprechende saisonale ARIMA-Modell anzupassen. Hier gibt das Argumentorder die Parameter(p, d, q)an, während das Argumentseasonal_orderdie saisonale Komponente(P, D, Q, S)des saisonalen ARIMA-Modells angibt. Nach dem Anpassen jederSARIMAX()+`model, the code prints out its respective `+AIC Punktzahl.

Da einige Parameterkombinationen zu numerischen Fehlern führen können, haben wir Warnmeldungen explizit deaktiviert, um eine Überlastung der Warnmeldungen zu vermeiden. Diese falschen Angaben können auch zu Fehlern führen und eine Ausnahme auslösen. Wir stellen daher sicher, dass diese Ausnahmen abgefangen werden und die Parameterkombinationen, die diese Probleme verursachen, ignoriert werden.

Der obige Code sollte die folgenden Ergebnisse liefern, dies kann einige Zeit dauern:

Die Ausgabe unseres Codes legt nahe, dassSARIMAX(1, 1, 1)x(1, 1, 1, 12) den niedrigstenAIC-Wert von 277,78 ergibt. Wir sollten dies daher als optimale Option unter allen Modellen betrachten, die wir in Betracht gezogen haben.

[[Schritt 5 - Anpassen eines Arima-Zeitreihenmodells]] == Schritt 5 - Anpassen eines ARIMA-Zeitreihenmodells

Mithilfe der Rastersuche haben wir den Parametersatz ermittelt, der das am besten zu unseren Zeitreihendaten passende Modell ergibt. Wir können dieses spezielle Modell genauer analysieren.

Wir beginnen damit, die optimalen Parameterwerte in ein neuesSARIMAX-Modell einzufügen:

Das Attributsummary, das sich aus der Ausgabe vonSARIMAX ergibt, gibt eine erhebliche Menge an Informationen zurück. Wir konzentrieren uns jedoch auf die Koeffiziententabelle. Die Spaltecoef zeigt das Gewicht (d.h. Bedeutung) jedes Features und wie sich jedes auf die Zeitreihen auswirkt. Die SpalteP>|z| informiert uns über die Bedeutung jedes Merkmalsgewichts. Hier hat jedes Gewicht einen p-Wert, der niedriger oder nahe an0.05 liegt, daher ist es sinnvoll, alle in unserem Modell beizubehalten.

Beim Anpassen von saisonalen ARIMA-Modellen (und anderen Modellen) ist es wichtig, eine Modelldiagnose durchzuführen, um sicherzustellen, dass keine der vom Modell getroffenen Annahmen verletzt wurde. Mit dem Objektplot_diagnosticskönnen wir schnell Modelldiagnosen erstellen und ungewöhnliche Verhaltensweisen untersuchen.

Unser Hauptanliegen ist es, sicherzustellen, dass die Residuen unseres Modells nicht korreliert und normal mit dem Mittelwert Null verteilt sind. Wenn das saisonale ARIMA-Modell diese Eigenschaften nicht erfüllt, ist dies ein guter Hinweis darauf, dass es weiter verbessert werden kann.

In diesem Fall deutet unsere Modelldiagnose darauf hin, dass die Modellreste normalerweise auf der Grundlage der folgenden Faktoren verteilt sind:

Diese Beobachtungen lassen uns den Schluss zu, dass unser Modell eine zufriedenstellende Anpassung ergibt, die uns helfen könnte, unsere Zeitreihendaten zu verstehen und zukünftige Werte vorherzusagen.

Obwohl wir eine zufriedenstellende Anpassung haben, können einige Parameter unseres saisonalen ARIMA-Modells geändert werden, um die Modellanpassung zu verbessern. Beispielsweise hat unsere Rastersuche nur eine eingeschränkte Anzahl von Parameterkombinationen berücksichtigt, sodass wir möglicherweise bessere Modelle finden, wenn wir die Rastersuche erweitern.

[[Schritt-6 -—- Validieren von Prognosen]] == Schritt 6 - Validieren von Prognosen

Für unsere Zeitreihen haben wir ein Modell erhalten, mit dem nun Prognosen erstellt werden können. Wir beginnen mit dem Vergleich der vorhergesagten Werte mit den realen Werten der Zeitreihen, um die Genauigkeit unserer Vorhersagen besser verstehen zu können. Mit den Attributenget_prediction() undconf_int() können wir die Werte und zugehörigen Konfidenzintervalle für Vorhersagen der Zeitreihen erhalten.

Der obige Code erfordert, dass die Prognosen im Januar 1998 beginnen.

Das Argumentdynamic=Falsetellt sicher, dass wir Prognosen mit einem Schritt voraus erstellen. Dies bedeutet, dass Prognosen an jedem Punkt unter Verwendung des vollständigen Verlaufs bis zu diesem Punkt erstellt werden.

Wir können die realen und prognostizierten Werte der CO2-Zeitreihe zeichnen, um zu beurteilen, wie gut wir abgeschnitten haben. Beachten Sie, wie wir das Ende der Zeitreihe durch Schneiden des Datumsindex vergrößert haben.

Insgesamt stimmen unsere Prognosen sehr gut mit den wahren Werten überein und zeigen einen allgemeinen Anstiegstrend.

Es ist auch nützlich, die Genauigkeit unserer Prognosen zu quantifizieren. Wir werden den MSE (Mean Squared Error) verwenden, der den durchschnittlichen Fehler unserer Prognosen zusammenfasst. Für jeden vorhergesagten Wert berechnen wir seinen Abstand zum wahren Wert und quadrieren das Ergebnis. Die Ergebnisse müssen quadriert werden, damit sich positive / negative Differenzen bei der Berechnung des Gesamtmittelwerts nicht ausgleichen.

Die MSE unserer One-Step-Ahead-Prognosen ergibt einen Wert von0.07, der sehr niedrig ist, da er nahe bei 0 liegt. Ein MSE von 0 würde bedeuten, dass der Schätzer Beobachtungen des Parameters mit perfekter Genauigkeit vorhersagt. Dies wäre ein ideales Szenario, aber normalerweise nicht möglich.

Mit dynamischen Vorhersagen kann jedoch eine bessere Darstellung unserer wahren Vorhersagekraft erzielt werden. In diesem Fall verwenden wir nur Informationen aus der Zeitreihe bis zu einem bestimmten Zeitpunkt. Danach werden Vorhersagen unter Verwendung von Werten aus vorherigen prognostizierten Zeitpunkten erstellt.

Im folgenden Codeabschnitt geben wir an, ab Januar 1998 mit der Berechnung der dynamischen Vorhersagen und Konfidenzintervalle zu beginnen.

Wenn wir die beobachteten und prognostizierten Werte der Zeitreihen zeichnen, sehen wir, dass die Gesamtprognosen auch bei Verwendung dynamischer Prognosen genau sind. Alle prognostizierten Werte (rote Linie) stimmen ziemlich genau mit der Grundwahrheit (blaue Linie) überein und liegen innerhalb der Konfidenzintervalle unserer Prognose.

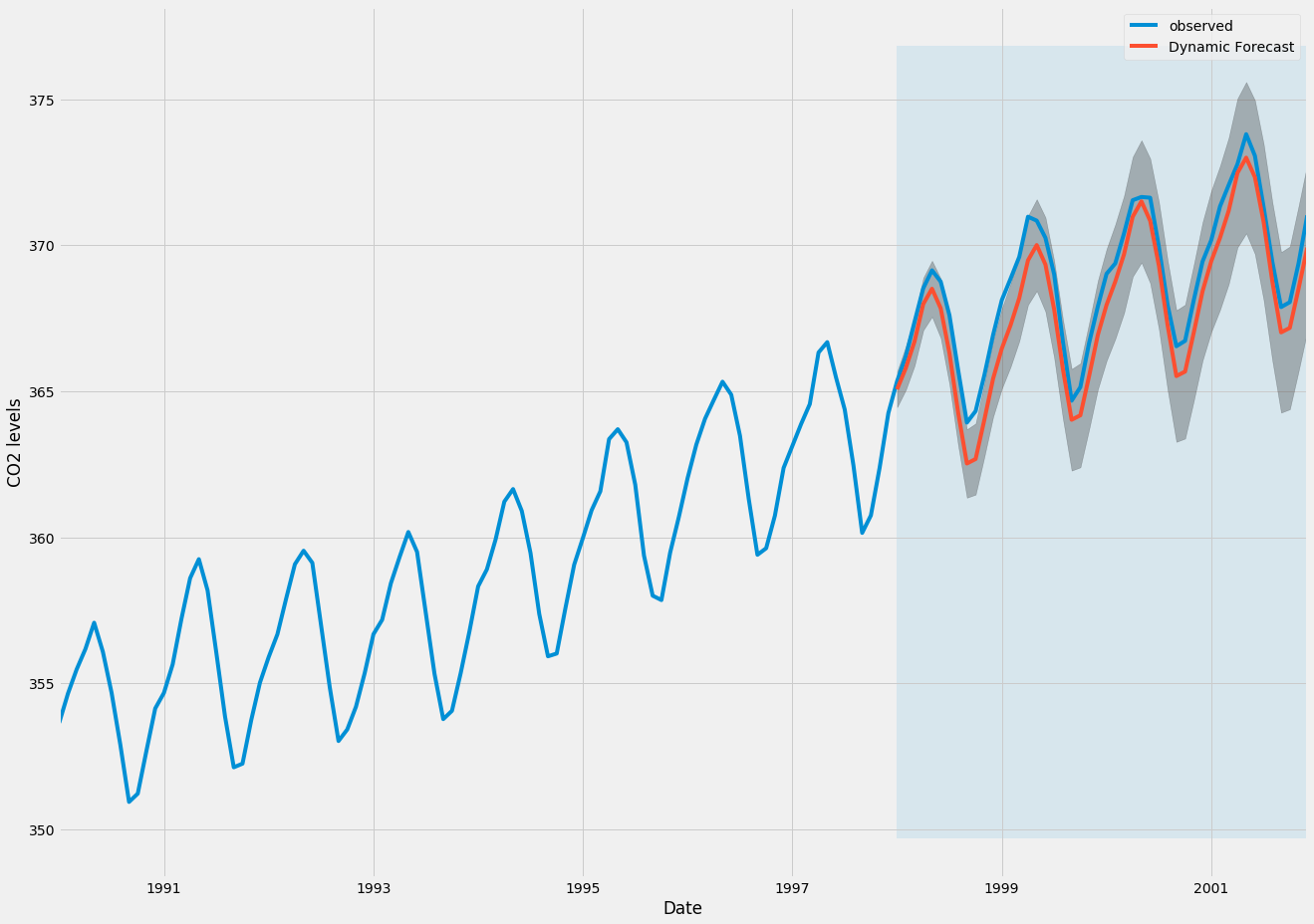
Wieder einmal quantifizieren wir die prädiktive Leistung unserer Prognosen durch Berechnung der MSE:

Die vorhergesagten Werte, die aus den dynamischen Vorhersagen erhalten werden, ergeben einen MSE von 1,01. Dies ist etwas höher als der Ein-Schritt-Vorsprung, was zu erwarten ist, da wir uns auf weniger historische Daten aus den Zeitreihen stützen.

Sowohl die einstufige Prognose als auch die dynamische Prognose bestätigen, dass dieses Zeitreihenmodell gültig ist. Das Hauptinteresse bei der Vorhersage von Zeitreihen liegt jedoch in der Möglichkeit, zukünftige Werte rechtzeitig vorherzusagen.

[[Schritt-7 - Erstellen und Visualisieren von Prognosen] == Schritt 7 - Erstellen und Visualisieren von Prognosen

Im letzten Schritt dieses Tutorials beschreiben wir, wie Sie unser saisonales ARIMA-Zeitreihenmodell nutzen können, um zukünftige Werte vorherzusagen. Das Attributget_forecast() unseres Zeitreihenobjekts kann prognostizierte Werte für eine bestimmte Anzahl von Schritten voraus berechnen.

Wir können die Ausgabe dieses Codes verwenden, um die Zeitreihen und Prognosen seiner zukünftigen Werte zu zeichnen.

Sowohl die Prognosen als auch das damit verbundene Konfidenzintervall, die wir generiert haben, können nun verwendet werden, um die Zeitreihen besser zu verstehen und vorherzusagen, was zu erwarten ist. Unsere Prognosen zeigen, dass die Zeitreihen voraussichtlich stetig zunehmen werden.

Wenn wir in die Zukunft blicken, ist es für uns selbstverständlich, dass wir unseren Werten weniger vertrauen. Dies spiegelt sich in den Konfidenzintervallen unseres Modells wider, die mit zunehmender Zukunft größer werden.

In diesem Tutorial wurde beschrieben, wie Sie ein saisonales ARIMA-Modell in Python implementieren. Wir haben die Bibliothekenpandas undstatsmodels ausgiebig genutzt und gezeigt, wie Modelldiagnosen ausgeführt und Prognosen für die CO2-Zeitreihen erstellt werden.

Hier sind ein paar andere Dinge, die Sie versuchen könnten:

Für mehr Übung können Sie auch versuchen, einen anderen Zeitreihendatensatz zu laden, um Ihre eigenen Prognosen zu erstellen.